1. 変光星
明るさを変える星を変光星という。
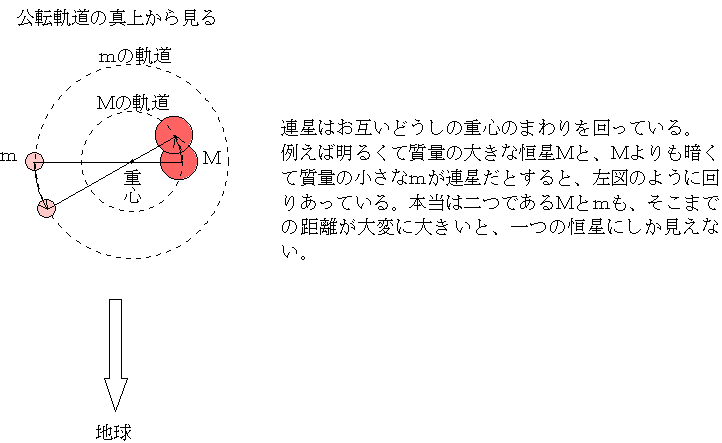
恒星の中にはお互い同士の引力で、お互い同士回りあっているものがある。これを連星という。連星の中には、地球からの距離遠すぎるため、連星であるそれぞれの恒星がまとめて一つの恒星に見えることがある。その連星の公転面の延長に地球があるとすると、地球から見てその連星がお互い同士を隠し合うような動きをする。すると二つの恒星の光の合計が変化する。そのときその連星は一つの恒星としか見えないので、その一つに見える恒星のみかけの明るさが変化するように見える。このような変光星(見かけ上の変光星)を食変光星という。もちろん望遠鏡を使えば、二つの恒星に分離できる場合もある。望遠鏡を使って分離できなくてくても、下のような変光曲線を描けば、これは食変光星(食連星)であることがわかる。

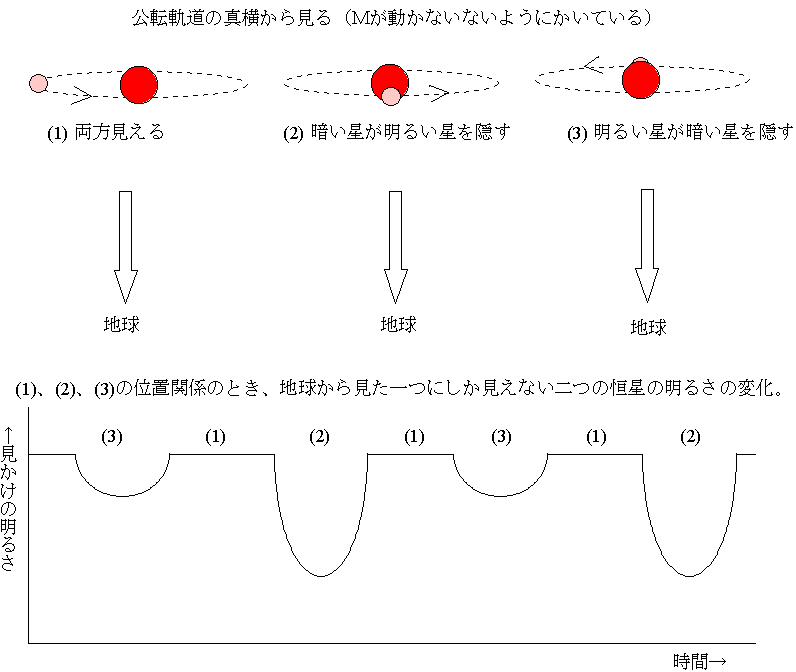
食変光星を含めた連星は、その運動の様子から、連星を構成しているそれぞれの恒星の質量を求めることができる。だから、連星は大変に重要である。
そして、質量がわかった恒星でその明るさを調べると、質量が大きいほど明るいという質量光度関係が求まるのである。本来は、連星系をなす恒星で質量光度関係が求められるわけだが、恒星の中のかなりの部分(20%〜30%程度)が連星系をなしているので、連星でない恒星でも質量光度関係が成り立つと考える。こうして、この質量光度関係を使って、主系列星ならばその明るさ(絶対等級)から質量を求めることになる。
b.脈動変光星
恒星が何らかの原因で、膨張・収縮を繰り返すようになることがある。このとき表面温度は変わらないので、膨張したときは明るくなり、収縮したときは暗くなる。このような変光星を脈動変光星という。一般に、脈動変光星は明るくなるときは急激に、暗くなるときはゆっくり暗くなることが多い。巨星は不安定なので、脈動変光星になっていることが多い。
食変光星と脈動変光星の変光については、国立科学博物館の「宇宙の質問箱」も参照。
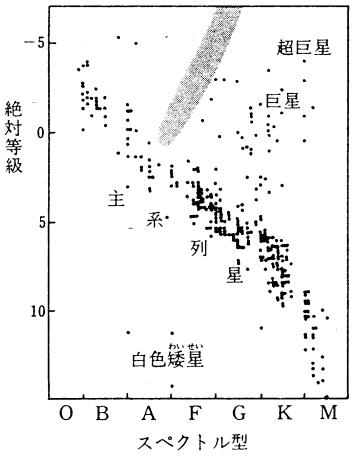 |
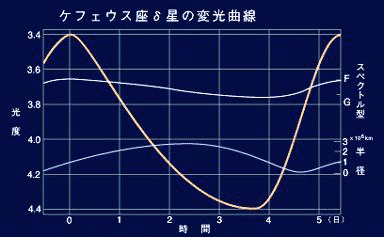 |
| HR図上でのケフェイド変光星の位置(網掛けの場所)、センター試験地学IB1995年追試験 | ケフェウス座δ星の変光曲線(半径やスペクトル型の変化にも注意):ニコンの星空案内(1999年9月。この号はすでに読めなくなっています。 http://www.nikon.co.jp/main/jpn/society/stars/stars199909.htm) |
脈動変光星にはいろいろなタイプのものがあるが、注目されるのはケフェイド変光星(ケフェウス型変光星)と呼ばれるタイプである。ケフェイド変光星は、変光周期1日〜50日、スペクトル型はF型〜K型で、代表的なものとしてケフェウス座δ(デルタ)星がある。このケフェイド変光星の大きな特徴は、変光周期の長いものほど明るいという変光周期光度関係があることである。つまり、変光周期を測るだけで絶対等級(変光しているのでその平均)がわかる。絶対等級がわかれば見かけの等級と比較することによって距離を求めることができる。スペクトル型(表面温度)があまり違わなければ、大きなケフェイド変光星ほど明るく、大きなケフェイド変光星ほど膨張・収縮に時間がかかるので、変光周期が長くなる。
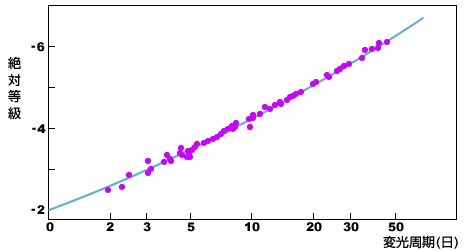
ケフェイド変光星の変光周期光度関係(国立科学博物館「宇宙の質問箱」)
http://www.kahaku.go.jp/exhibitions/vm/resource/tenmon/space/galaxy/galaxy05.html
ケフェイド変光星の変光周期光度関係を使った距離の測定は、年周視差、分光視差の方法では距離を求めることができないような遠い星雲、銀河までの距離を求めるときに使われる。
ただし、種族I、種族IIという恒星のタイプの違いによる変光周期光度関係の違いがある(種族Iの方が少し明るい)ので注意が必要である。
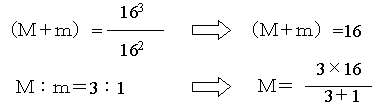
恒星の質量:質量Mと質量mである恒星がr(AU)という距離を、周期T(年)で回っているとする。ここでAUは天文単位で、地球−太陽間の距離を1とする距離の単位である。すると、この連星系でもケプラーの第3法則が成り立つ。
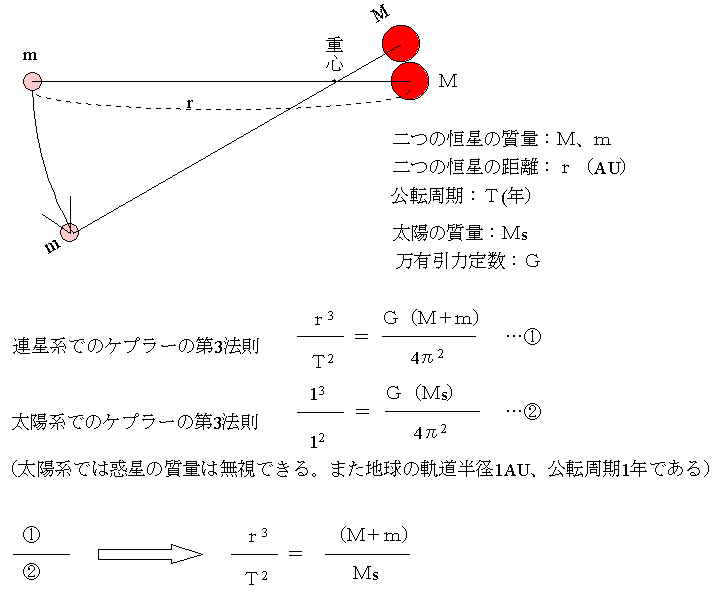
このように、連星間の距離、連星がお互いを回りあっている公転周期がわかれば、その連星をなしている恒星の質量の合計が太陽の何倍であるかがわかる。二つの恒星の質量を分離するには、それぞれの恒星が重心からどのような距離にあるかがわかればよい。つまり、重心は二つの恒星間の距離を質量の逆比に内分する場所であることを利用する。そのとき、M×a2=m×a1である。
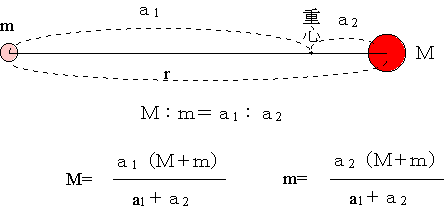
たとえば、16AUの距離を16年で回っている連星があるとすると、その質量の合計は太陽の16倍。また、この連星系の重心から質量の大きな恒星恒星までの距離:質量の小さな恒星までの距離=3:1ならば、質量の大きな恒星は太陽の12倍の質量を持っていることになる。質量の小さい方は太陽の4倍となる。