| このページの目次 | |
| 第5章 恒星(1) | |
| 1. 恒星までの距離(1) | |
| 用語と補足説明 | |
| 参考になるサイト | |
1. 恒星までの距離(1)
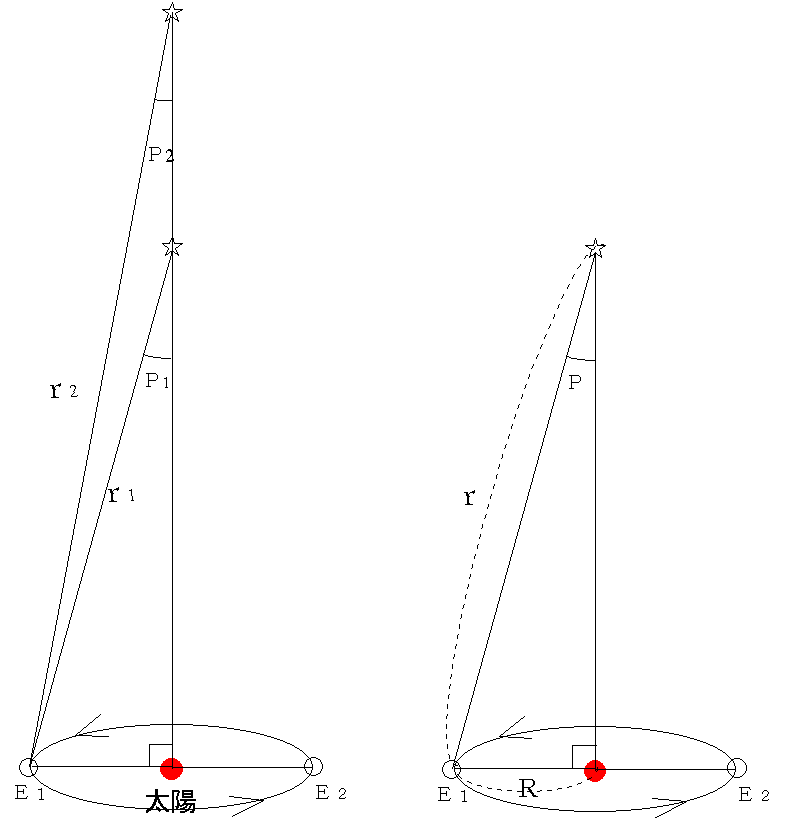
地球は太陽のまわりを公転しているため、同じ恒星を半年後には地球と太陽の距離の2倍の3.0×108km(3億km)離れた位置から見ることになり、視差を生ずる。これが年周視差であった。年周視差は地球に近い恒星ほど大きく、地球から遠い恒星ほど小さい(下の左図でr1<r2のときP1<P2)。

上の右図のように、地球−太陽間の距離をR、地球−恒星間の距離をrとすると、sinP=R/r。だから、r=R/sinPとなる。しかし、角度Pをラジアンという単位で測ると、Pが非常に小さいときはsinP=Pである。恒星の年周視差は非常に小さく、最大のケンタウルス座α星でもその値は0.742″(秒)である。1″=4.85×10-6rad(ラジアン)という小さい値なので、恒星の年周視差(rad)は1万分の1radよりも小さい。
※ 1°=60′(分) 1′=60秒 つまり、1°=3600″
年周視差をrad(ラジアン)という単位で測れば、 r=R/sinP → r=R/P となる。なお、sin(サイン)については、三角比と三角関数のページを参照。
これは、R(地球−太陽間の距離)は一定だから、年周視差と恒星までの距離は反比例の関係にあることを意味している。
いま、年周視差をrad(ラジアン)という単位で測ったが、radと日常生活でよく使う<°>(360°法の°)は比例関係(1°=2π/360(rad)=1.74×10-2radという関係)にあるので(ラジアンの項参照)、角度の単位を<°>(360°法の°)で測っても、年周視差と恒星までの距離は反比例の関係にある。
ここで発想を変えて、年周視差と恒星までの距離は反比例の関係にあるのだから、その比例定数が最も簡単な1となるような距離の単位をつくってしまう。つまり、年周視差1″になるような距離を1とする単位を決めてしまうのである。これがパーセク(pc)という単位である。
年周視差が1″となる距離=1pc。年周視差と恒星までの距離は反比例するので、年周視差がP(″)であるような恒星までの距離は
r(pc)=1/P(″) ※ pcとkmなどとの換算は下を参照。
つまり、年周視差(″)を測定できれば、恒星までの距離(pc)を求めることができる。しかし、年周視差は大変に小さい値なので、現在の技術でも測定できるのは、地上からの観測では1/100″程度でしかない。距離にして100pc程度でしかない。
大気圏外に出れば大気の揺らぎがないので、もう少し小さい値でも測定できる。こうした目的で打ち上げられたのが、欧州宇宙局(ESA)の天体観測衛星「ヒッパルコス」である(1989年6月打ち上げ)。ヒッパルコスは当初の静止軌道に乗らなかったため、観測データの解析が大変だったようであるが、約12万個の恒星の年周視差を0.001秒の精度で求めた(国立天文台「天文ニュース第91号」(1997年3月13日)参照)。つまり、1000pc(3260光年)以内に位置する恒星の距離を正確に求めたことになる。
地球(太陽系)に一番近い恒星はケンタウルス座α星で年周視差0.742″(1.35pc、4.4光年)、ついでバーナード星の年周視差0.549″(1.82pc、5.9光年)である。シリウスも近い恒星(第7位)で、年周視差0.379″(2.64pc、8.6光年)である。
しかし、1000pcよりも遠い恒星・天体までの距離は、年周視差を測定できないので、この方法では求まらない。こうした年周視差が測定できないような遠い天体までの距離は、分光視差、ケフェイド変光星(ケフェルス型変光星)の周期光度関係、銀河の平均光度(-21等級)、ハッブルの法則などから求める。だが、これらの方法は年周視差の方法ほど直接的なものではない。
太陽からの光は地球まで8分20秒で届く。その光で一番近い恒星まで4.4年、地球−太陽間の距離の約30万倍(28万倍)もある。太陽の半径が6.69×105km(地球の半径の約110倍)だから、一番近い恒星まではその半径の6億倍以上、地球の半径の約600億倍以上もある。宇宙がいかに「すかすか」かがよくわかる。
pcとkmや光年:sin1″=sin4.85×10-6rad。4.85×10-6は大変に小さい値なので、この値をsinの値としてよい。つまり、sin1″=4.85×10-6となる。よって、年周視差1″の恒星までの距離は、地球-太陽は1.5×108kmだから
r(1pc)=1.5×108km/4.85×10-6→ 1pc=3.09×1013km(約30兆km)。
また、秒速3.0×105kmの光が1年(3.16×107秒)かかって進む距離が1光年(ly)である。
1光年=3.0×105km/秒×3.16×107秒=9.47×1012km。
1pc=3.09×1013km÷9.47×1012km=3.26光年。