| このページの目次 | ||
| 第5章 恒星(2) | ||
| 2. 恒星の明るさと等級 | ||
| a.見かけの明るさ(見かけの等級) | ||
| b.絶対等級 | ||
| 3. 見かけの明るさと絶対等級と距離の関係 | ||
| 用語と補足説明 | ||
| 参考になるサイト | ||
2. 恒星の明るさと等級
昔の人は肉眼で見て、もっとも明るい恒星の一群を1等星(1等級の明るさの星)とし、肉眼でやっと見える明るさの恒星を6等星とし、その間の恒星を2等〜5等と定めた。これを見かけの等級という。見かけの等級は実視等級ということもある。
恒星からの光を正確に測ることができるようになって調べてみると、1等星の明るさは、6等星の明るさのちょうど100倍であることがわかった。さらに、どの等級どおしの差が1等級増えるごとに、明るさは約1/2.5ずつ暗くなることもわかった。
現在では、1等星の明るさを2.5倍明るければ0等星、0等星より2.5倍明るければ-1等星、さらに2.5倍明るければ-2等星と定義を拡張している。一番明るく見える恒星シリウスは-1.6等星である。また、恒星以外の太陽系の天体についてもこの等級をつかう。たとえば、もっとも明るいときの金星は-4.5くらいにまでなる。満月の月は-12.6、太陽は-27である。
望遠鏡を使えば、6等星よりも暗い星を見ることができる。6等星より1/25ずつ暗くなれば、7等、8等、…、となる。現在では巨大望遠鏡と、フィルムやCCD(半導体)などで光をためることによって、26等星よりも暗い天体を見ることができるようになっている。5等級大きくなると明るさは1/100になるのだから、26等星は1等星の100億分の1の明るさでしかない。さらに、国立天文台がハワイに建設した巨大望遠鏡“すばる”では、見かけの等級で27〜28等級までの明るさがとらえられるという。
では1等級違うと、なぜ明るさは2.5倍ずつ違うのだろう。1等星の明るさをL1、2等星の明るさをL2、…、6等星の明るさをL6とする。
1等級と3等級、1等級と4等級、2等級と5等級、2等級と6等級などの明るさの比は下のようになる。
つまり等級の差が1なら約2.5倍、差が2なら2.52の約6.3倍、差が3なら2.53の約15倍、差が4なら2.54の約39倍となる。
上の式を見てみると、100の5分の何乗の部分に等級の差が現れていることがわかる。つまり、m等級の明るさLm、M等級の明るさLMとすると、その明るさの比は下のようになる。
等級の差が5であれば(たとえば5等星と10等星)、明るさの比は100倍。等級の差が10であれば、1002の10000(1万)倍。等級の差が15であれば1003の1000000(100万倍)となる。
b.絶対等級
恒星までの距離は恒星それぞれによって異なる。だから、地球上のわれわれから見て、本当は明るい恒星でもその恒星までの距離が非常に遠ければ、見かけの明るさ(見かけの等級)は暗い。逆にわれわれからの距離が近ければ、見かけの明るさは明るい。
恒星の本当の明るさを比べるために、それぞれの恒星をみな10pcという距離離れて見たとしたときの明るさで比べる。これが絶対等級である。
地球から見ると-27等の太陽も、10pc離れてみるとすると5等級の明るさになる。つまり、太陽の絶対等級は5である。
ある光源からの距離を2倍にすると、同じ光の量(エネルギー)で照らさなくてはならない面積は4倍、距離を3倍にすると9倍、4倍にすると16倍になる。つまり、一定の面積(ある同じ面積)に来る光の量は距離を2倍、3倍、4倍にすると、1/4、1/9、1/16になる。こうして、見かけの明るさは距離の2乗に反比例していることがわかる。
ここで、100pcの距離にある恒星の見かけの等級が10等級だとする。これを10pcの距離で見たらどうなるかを考える。つまり、その恒星の絶対等級を考える。距離が1/10になるのだから、見かけの明るさは100倍になる。明るさの比が100倍ということは、等級の差が5ということである。見かけの明るさは距離が近くなれば明るくなる。明るくなるということは、等級では小さくなることに注意すると、この恒星の絶対等級は5であることがわかる。
同じように考えて、距離1000pc、10000pc、100000pc、あるいは1pc、10pcでの見かけの等級(m)と絶対等級(M)の差の表をつくると下のようになる。
| 距離(pc) | 1 | 10 | 100 | 1000 | 10000 | 100000 | 1000000 |
| m-M | -5 | 0 | 5 | 10 | 15 | 20 | 25 |
例えば、距離が10000pcの恒星の見かけの等級(m)が12であったとすると、上の表から絶対等級(M)を求めることができる。
12−M=15 → M=-3(絶対等級-3)
逆に、もし何らかの方法でその恒星の絶対等級がわかれば、見かけの等級はその恒星を見てやればわかるので、上の表からその恒星までの距離を求めることができる。
例えば、見かけの等級(m)が18の恒星の絶対等級(M)が3だとわかったとする。m-Mの値が15なので、上の表から、その恒星までの距離は10000pcであることがわかる。
m-Mの値が5の倍数にならない一般の場合は下を参照。
4等級の明るさの違い:5等級違うと明るさは100倍の違いある。そして1等級ごとに約2.5倍異なる。だから、4等級の差は100倍よりも、その比は1/2.5になる。つまり4等級の差は約40倍の明るさの違いとなる。
恒星までの距離:見かけの等級(m)と絶対等級(M)、距離r(pc)の関係を考える。rpc離れた恒星の見かけの等級をm、地球上での明るさをLm、その恒星を10pcの距離に持ってきたときの明るさ(つまり絶対等級)をM、その時の地球上での明るさをLMとする。なお、対数については対数のページを参照。
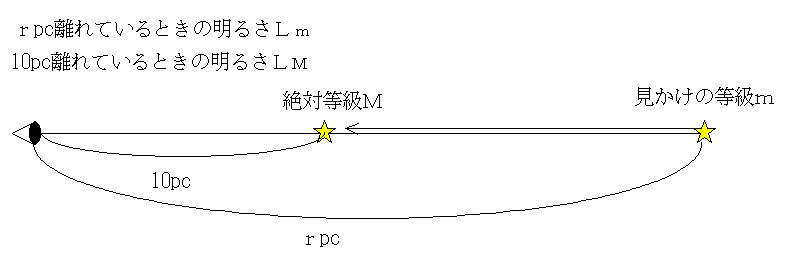
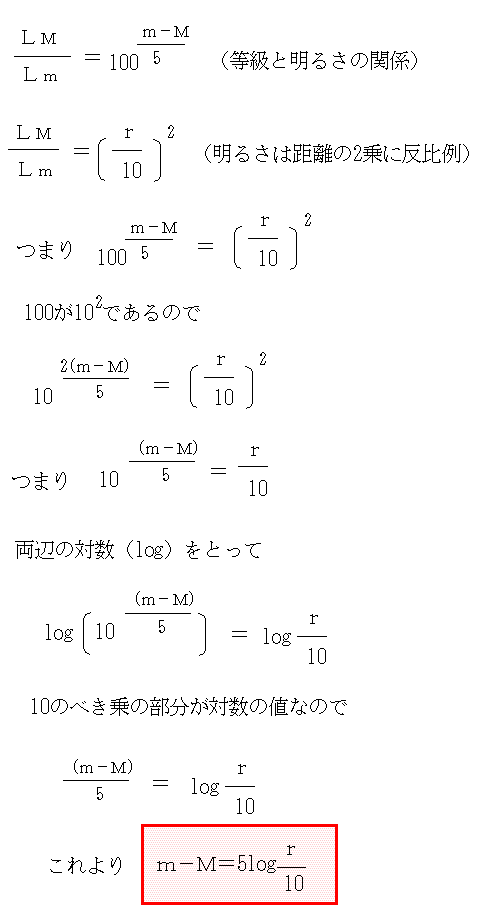
この式は大変に重要な式である。年周視差を観測で求めることできないような遠い恒星(天体)については、何らかの方法でその恒星(天体)の絶対等級を推定し、この式から距離(pc)を求めるのである。