8. 分光視差(恒星までの距離(2))
HR図を見てわかることは、主系列星ならばそのスペクトル型からおおよその絶対等級がわかるということである。例えば、G型の主系列星ならば、その絶対等級はおよそ5であるとわかる。だから、何らかの方法で、その恒星が主系列星である、逆にいえば巨星や白色わい星ではないということが確認できれば、スペクトル型から絶対等級を推定できる。絶対等級がわかれば、見かけの等級と比較することによって、その恒星までの距離を求めることができる。
では、どうやってその目的の恒星が主系列星であるとわかるのだろう。恒星のスペクトルはその恒星の大気の状態によって特徴が出る。主系列星と比べて、巨星は大変に密度が小さく、逆に白色わい星は密度が非常に大きい。だから、例えば同じK型の恒星でも主系列星と巨星では、また同じA型の恒星でも主系列星と白色わい星では、そのスペクトルに違いが出る。だから、スペクトルの特徴によってその恒星が主系列星かどうかが判断できるのである。
このように、スペクトル型から絶対等級を推定し、見かけの等級との比較で距離を求める方法を分光視差の方法という。この分光視差の方法では、年周視差の測定が必要ない。つまり、年周視差が測定できないような遠い恒星までの距離も求めることができる。
9.恒星の動き
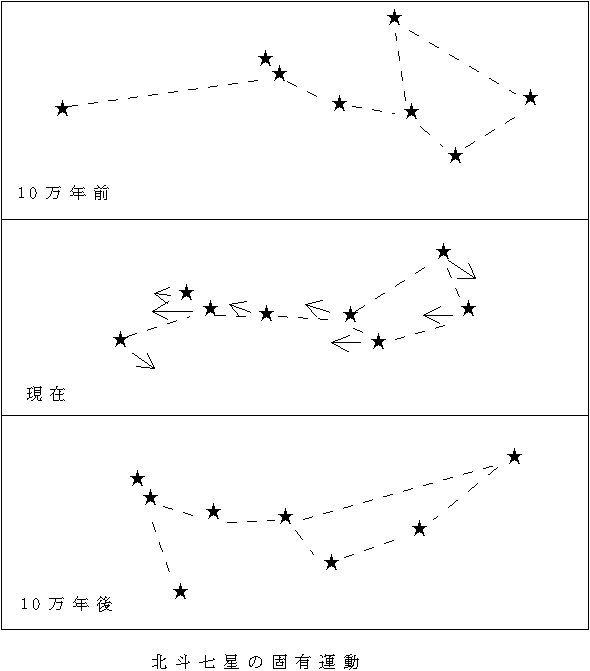
星座を考えることができることからもわかるように、恒星はお互いどおしの位置をほとんど変えない。だが、詳しく観測すると恒星自身の動きがわかる。たとえば、北斗七星も長い年月の間には、下の図のように変形する。このような恒星の動きを固有運動という。

だが恒星はわれわれに向かう向きにも、近づいてきたり、遠ざかったりという運動をしている。これが視線速度である。固有運動は視線速度に対して垂直な向きの運動である。
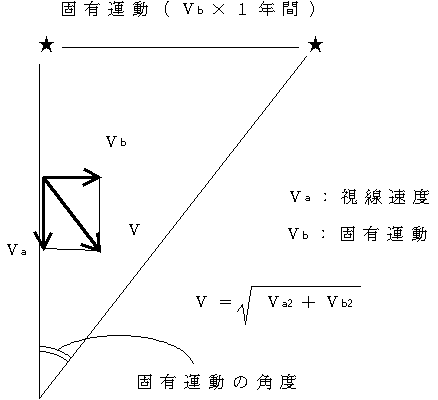
だから、実際の恒星の動きはその二つの動きを合成したものになる(上図参照)。
固有運動は、長い時間間隔を開けた観測を行って、ある一つの恒星の天球上での位置のずれを調べる。固有運動とその恒星までの距離から接戦方向(視線方向に垂直な向き)の実際のずれの量がわかるので、観測の時間間隔で割ることにより速度がわかる。視線速度は光のドップラー効果を利用して測定する。こうして恒星の運動(![]() )がわかるのである。
)がわかるのである。
主系列星であることの確認:恒星は集団をつくることが多い。この集団を星団という。星団に属する恒星一つ一つの距離の違いが無視できるような遠い星団を考える。この星団に対して、見かけの等級とスペクトル型で仮のHR図を作ってみる。すると、左の上から右下に並ぶ主系列星がはっきりと出てくる。
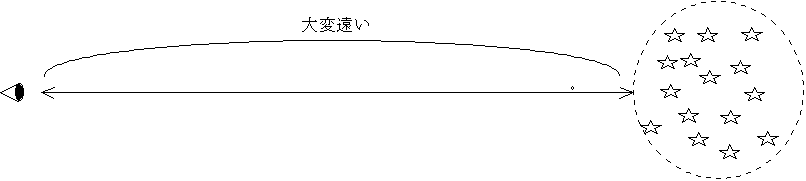
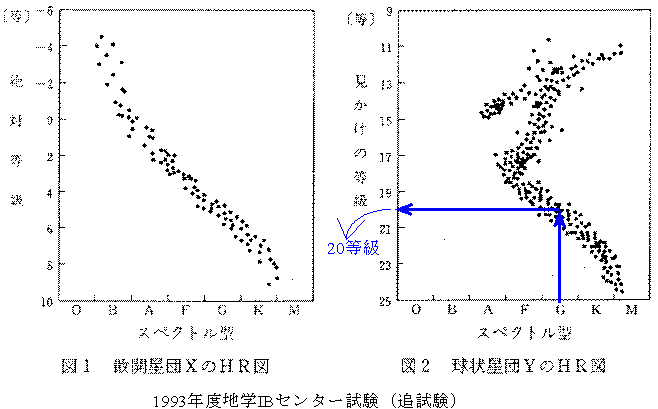
左の散開星団Xの場合は、われわれからの距離が小さいので、年周視差が測定できる、つまり距離がわかるので絶対等級もわかる場合である。右の球状星団Yのわれわれからの距離が大きいので、年周視差が測定できない、つまり距離がわからないので、まず仮に見かけの等級とスペクトル型でHRを作っている。
この右のHR図でも左の上から右下に並んでいる一群の恒星、つまり主系列星があることがわかる(左上にあるべきO型、B型の主系列星はない、これについては恒星の進化を参照)。そこで、主系列星のG型の見かけの等級(m)が20等級と読める。主系列星でG型の恒星の絶対等級(M)は5等級であった。両者の差m-M=15、これは見かけの等級と絶対等級の差と距離の表から、10000pc(32600光年)の距離にある星団であることがわかる。
このように、星団の場合は見かけの等級とスペクトル型で仮のHR図をつくると主系列星が浮き出てくる。
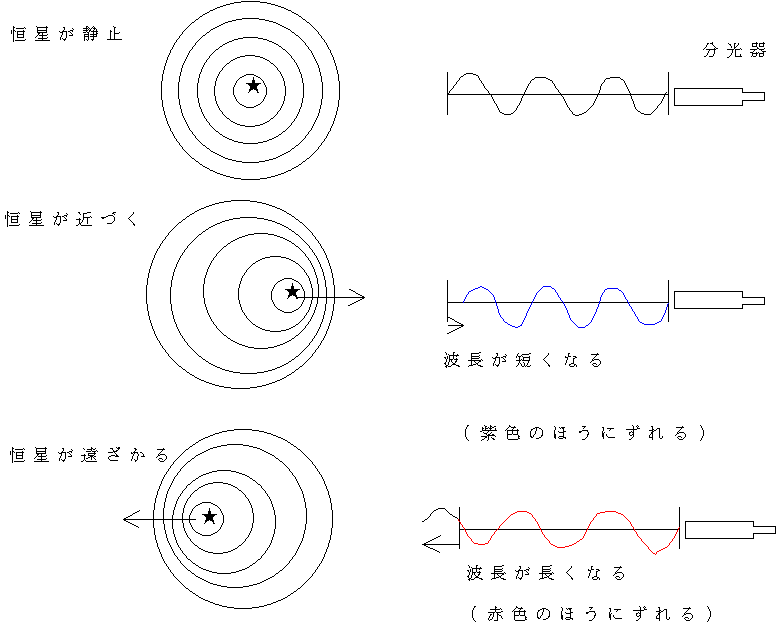
ドップラー効果:近づいてくる救急車の「ピーポー音」は音程が高く聞こえ、遠ざかる救急車の「ピーポー音」は音程が低く聞こえる。音程が高いということは音波の波長が短いということ、音程が低いということは音波の波長が長いということである。つまり、音源が近づいてくるときは音波の波長が短くなり、音源が遠ざかるときは音波の波長が長くなる。
光でも同じである。光源(恒星)が近づいてくるときは光の波長が短くなり(青い方にずれる)、遠ざかるときは光の波長が長くなる(赤い方にずれる)。本来の光の波長λ(ラムダ)、ずれをΔλ(デルタ・ラムダ)、われわれに対する速度v、光速cとすると Δλ/λ=v/c となる。この波長のずれは、特定の元素の暗線(吸収線)を利用すると厳密に決めることができる。なお、われわれに対する速度が光速に対して無視できないときは、こちらを参照。
このように、光のドップラー効果を利用すると、恒星のわれわれに対する方向(視線方向)の動き(速度)を求めることができる。現在では、秒速15mの動き(光速の2万分の1の速さ)までが測定できるという(「異形の惑星」井田茂、NHKブックス、2003年4月)。
なお、ドップラー効果や赤方変位のアニメーションはこちらを参照。