c.ケプラーの法則
ケプラー(1571年〜1630年)は、チコ・ブラーエ(1546年〜1601年)が残した太陽系の惑星の観測資料を研究して、1609年に第1法則、第2法則を発表し、10年後の1619年に第3法則を発表した。
ケプラーの法則
| 第1法則(だ円軌道の法則) | 惑星は太陽を一つの焦点とするだ円軌道上を動く。 |
| 第2法則(面積速度一定の法則) | 惑星と太陽を結ぶ線分が、一定時間に描く面積は一定である。 |
| 第3法則(調和の法則) | 惑星の公転周期の2乗と惑星の太陽からの距離の3乗の比は、惑星によらず一定である。 |
c.-1. 第1法則
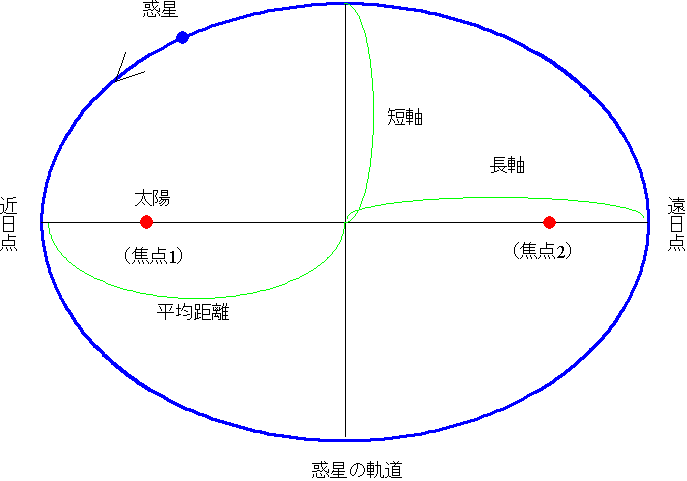
ケプラー以前は(コペルニクスも)惑星の運動は神が支配しており、神は完全無欠、また完全無欠な図形は円と直線しかないと考えられていたので、とうぜん惑星の軌道は円だと考えられていた。ケプラーはそうではなく、惑星の軌道はだ円(楕円)であり、しかもその中心に太陽があるのでもなく、中心からずれた位置にある焦点(の一つ)に太陽があるということを明らかにした。
なお、だ円についてはこちらを参照。また、第1法則の証明は高校までの理科(物理)の範囲を超える。
実際の惑星の軌道の離心率は、水星(0.2056)、めい王星(0.2490)以外は、火星の0.0934が最大である。ケプラーはチコ・ブラーエからも、「火星の軌道は円に合わせるのがもっとも難しい」ときいていた。ケプラーがまず火星の軌道を研究したのはよかった。しかし、火星でも離心率は小さいので、実際に火星のだ円軌道をきちんと決めるのは大変な作業である。ちなみに地球の軌道の離心率は0.0167である。水星やめい王星を含めて惑星の軌道はだ円といっても、非常に円に近いだ円である。だから、下の図はだ円を非常に強調した図である。

c−2. 第2法則
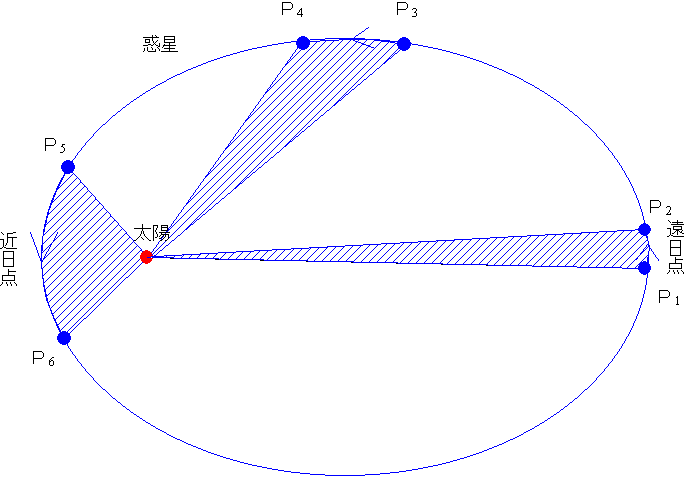
下図で、ある一定の時間の間に惑星がP1→P2、P3→P4、P5→P6と動くとする。そのとき下図の斜線をつけた部分の面積が等しいということである。つまり、惑星は太陽から遠いときはゆっくり動き、太陽に近いときは速く動くということである。このケプラーの第2法則により、惑星の軌道上のある位置での速さがきちんと計算できるようになった。
また、離心率の大きな極端なだ円軌道をもつ彗星でもケプラーの法則は成り立っていて、その軌道上の動き(太陽から遠いときは非常にゆっくり動き、太陽に近づくと大変に速く動く)ということも説明できる。
第2法則の証明は比較的簡単である。
c−3. 第3法則
惑星の公転周期をTとし、惑星と太陽の平均距離をaとすると、a3:T2の値はどの惑星でも一定ということになる。
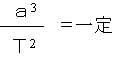
ここで、公転周期の単位として年、惑星と太陽の平均距離の単位として天文単位(AU)を使うと、地球の公転周期は1年、地球と太陽の平均距離は1AUなので、この比の値は1ということになる。
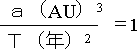
例えば、金星の公転周期は0.6152年、太陽との平均距離は0.7233AUだから比の値は0.9998、木星の公転周期は11.862年、平均距離は5.2026AUだから比の値は1.0008である。
このケプラーの第3法則によってはじめて、惑星の間の相互関係を求めることができるようになった。そして、太陽からの距離がわかると公転周期が、公転周期がわかると太陽からの距離がわかることになる。また、太陽からの距離と公転の速さの関係も求めることができる。その基本的な値となる、地球と太陽の距離もケプラーの第3法則から求めている。
ケプラーの第3法則の証明は、惑星の軌道をだ円ではなく円とすれば(じっさい離心率が小さいので円としてよい)、それほど難しくはない。ただし、円運動は何かを知っていることが前提である。本当は、このケプラーの第3法則をヒントとして、ニュートンは万有引力の法則(逆2乗則)を考え出したのである。リンゴが落ちるのを見たことがヒントになったかもしれないが。この件についてはニュートンのページも参照。
第2法則から軌道上の速さを求める:下図で、惑星がP1、P3、P5の位置にあるときの太陽からの距離をそれぞれa1、a2、a3、またそのときの公転の速度(矢印)をそれぞれv1、v2、v3とする。するとこのとき、ケプラーの第2法則から、太陽からの距離とそのときの速度がつくる三角形の面積(斜線の部分の面積)が等しいことがわかる。ここで、これらの2辺がなす角度がすべて直角だとすると、その面積は下のようになる。
※ 厳密には、例えばP3の位置で示したように、太陽からの距離a3とそのときの公転速度v3がつくる三角形(青色の斜線)は直角三角形ではないが、a3とv3を直角としたときの面積(緑色の斜線)とほとんど変わらない。(速度の矢印の相対的な大きさを保ったまま、全部の矢印を小さくすれば、この緑色と青色の三角形の面積は等しいと考えてよい。)
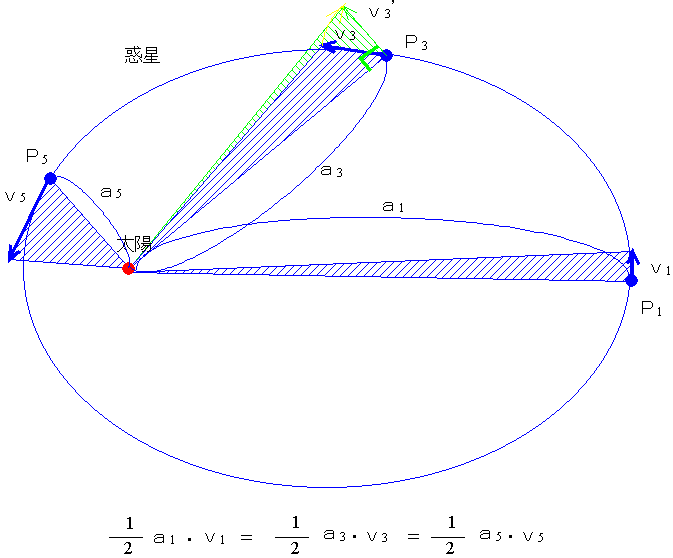
つまり、太陽からの距離とそのときの速度(の大きさ=速さ)の積は、惑星がどの位置にいても一定であるということを示している。つまり、太陽からの距離とそのときの速さは反比例の関係にある。
例えば、地球と太陽の平均距離(a)は1.496×108km、そのときの速さは29.78km・s-1である。そして、離心率(e)が0.0167なので近日点距離(a(1−e))は1.471×108km、遠日点距離(a(1+e))は1.521×108kmだから、それぞれの位置における速さは30.29km・s-1、29.29km・s-1であることがわかる。またハレー彗星は太陽からの平均距離18AU(離心率0.97)のだ円軌道を、76年の周期で回っている。だから、遠日点と近日点では公転の速さが(1+0.97)÷(1−0.97)=66倍も違うこともわかる。
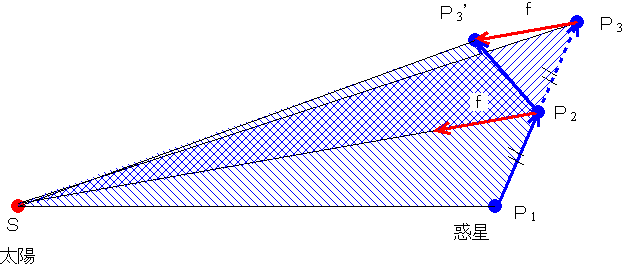
第2法則の証明:惑星に何も力が働かないと、その惑星は等速直線運動を続ける。だからあるときにP1の位置にいた惑星はP1→P2→P3と等速直線運動をする。ここで太陽の引力を考える。本当は太陽の引力は連続的に働いているわけだが、話を簡単にするために、ごく短い時間間隔をあけて断続的に働く(パッ、パッ、パッという感じで働く)とする。
惑星がP2の位置に太陽の引力(f)が働いたため、惑星の軌道が曲げられて、何も力が働かなかったらP3の位置に来たはずの惑星が、P3’の位置に来たと考える。
このときにできる三角形(斜線)の面積を考える。まず△SP1P2と△SP2P3は、頂点Sを共有し、P1P2=P2P3(等速直線運動だから)なので、底辺の長さが等しく、高さも同じ三角形。つまり △SP1P2=△SP2P3。
次に△SP2P3と△SP2P3’を比べる。二つの三角形は底辺SP2を共有している。またSP2とP3’P3は平行(P3P3’はP2で太陽Sに向かう力によって生じた加速度fに平行)なので高さも等しい。つまり、この二つの三角形の面積は等しい。△SP2P3=△SP2P3’。
結局、△SP1P2=△SP2P3=△SP2P3’だから、、△SP1P2=△SP2P3’。これを太陽のまわりのどの位置でも成立するので、ケプラーの第2法則が証明される。
※ 第2法則は、太陽の引力(太陽に向かう力=中心力)さえあれば成り立つ。つまり、万有引力のように距離の2乗に反比例する力でなくてもよいこともわかる。
第3法則の応用:例えば、太陽からの平均距離が4AUである位置に天体があるとすると、
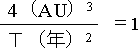
つまりT2=64 → T=8(年)であることがわかる。
また、ケプラーの第3法則は地球とそのまわりを回る月や人工衛星の間でも成り立つ。ここで、静止衛星の軌道を求めてみる。静止衛星とは地球のまわりを回る公転周期がちょうど1日なので、地球から見ると天のある場所にとどまって動かないように見える衛星のことである。
月の公転周期は(約)27日であり、静止衛星の公転周期は1日である。また月までの距離をaとして、静止衛星までの距離をxとする。
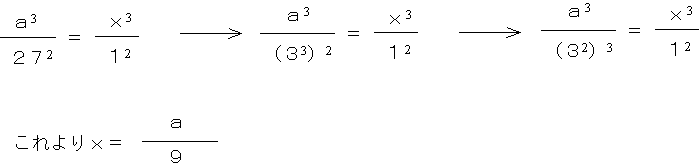
つまり、月までの距離の9分の1の高さに人工衛星を打ち上げると、その人工衛星は静止衛星になる。月までの距離は384400kmなので、地球の中心から静止衛星までの距離は42700km、地球の表面からだと約36000kmの高さということになる。逆に、地表からの高さが正確に求まる人工衛星の公転周期、さらには月の公転周期から、月までの距離を求めることもできる。
さらに、太陽からの距離と公転速度の関係を求めることもできる。
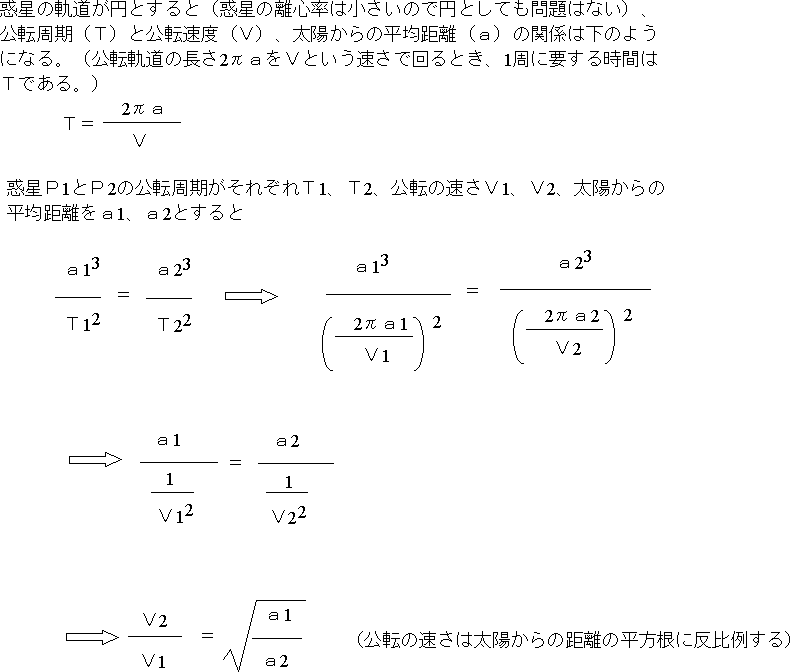
地球と太陽の距離:現在では、地球と太陽の距離はケプラーの第3法則から求めている。まず地球と金星の距離(a)を、電波の跳ね返りに要する時間から正確に求める。そして下のように地球と太陽の距離(x)、地球の公転周期(TE)、金星の公転周期(TV)の間にケプラーの第3法則を適用する。
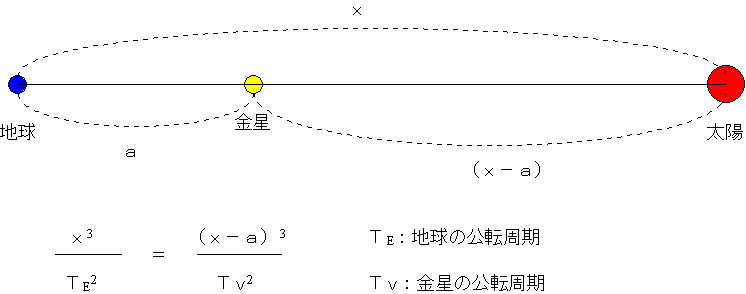
上の3次方程式を解けばよい。
※ 4次方程式までは根の公式(一般解)がある。5次方程式以上は根の公式(一般解)がない。
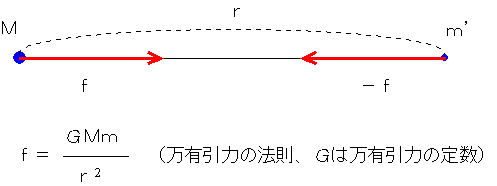
ケプラーの第3法則の証明:まず、ニュートンが発見した万有引力は、質量Mとmの物体は、質量の積に比例して、距離の2乗に反比例する大きさで、お互いを引き合う力である。このときの比例定数が万有引力の定数で、長さとしてメートル(m)、質量としてキログラム(kg)、時間として秒(s)という単位(SI単位系)を使うとその値はG=(6672.59±0.30)×10-14m3・s-2・kg-1(N・m2・kg-1)という値になる。
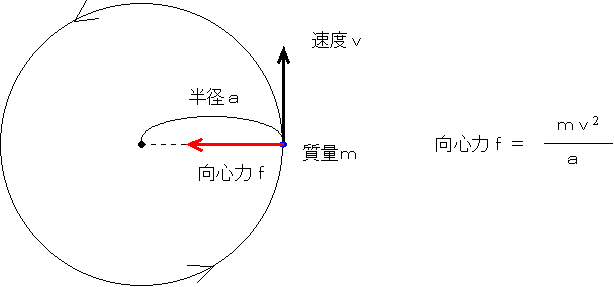
また、円運度とはある半径(a)で、ある質量(m)の物体が等速運動(vという速さ)をしているものである。このとき、この物体にはつねに中心に向かう力(向心力)が働いている。例えば糸におもりをぶら下げて、ぐるんぐるんと回せばおもりは円運動をする。このとき糸が引っぱる力(張力)が向心力として働いているわけである。惑星が太陽のまわりを回っているということは、太陽の引力が向心力として働いているということである。このとき、向心力は質量と速さの2乗に比例し、円運動の半径に反比例する力である(じつはこの向心力の大きさも、ニュートンが明らかにした運動の法則から導き出すことができる)。
もう一つ、ふつうは太陽のまわりを地球が回るとか、地球のまわりを月が回るといってしまうが、厳密にはお互いの重心のまわりを回り合っている。その重心の位置は、お互いの距離をお互いの質量の逆比で内分する点となる(下図)。つまり、重心からの距離×質量が同じ値になっている。
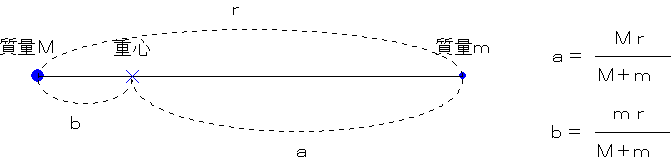
だから、天体どうしがお互いに回りあっているときは下の図のようになっている。質量の大きな天体SがS1→S2と動くとき、質量の小さい天体PはP1→P2と動くことになる。お互いの距離(万有引力が働く距離)と、円運動の半径が異なることに注意。
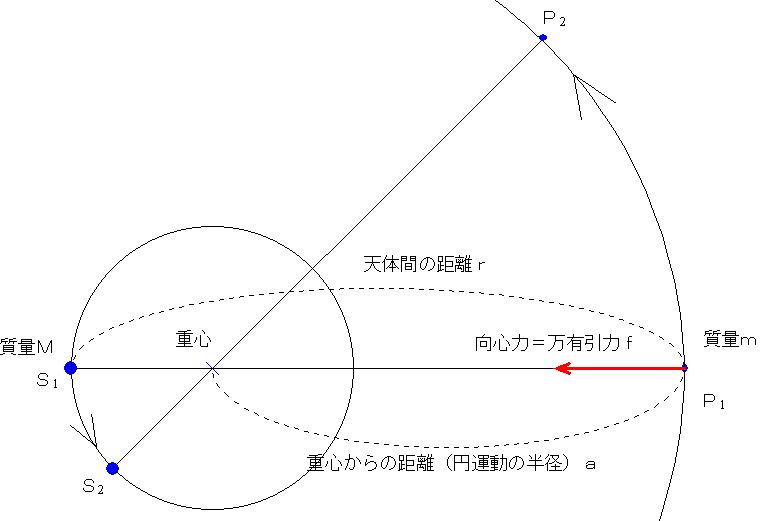
ここで、向心力=万有引力という式を立て、それを変形していく。
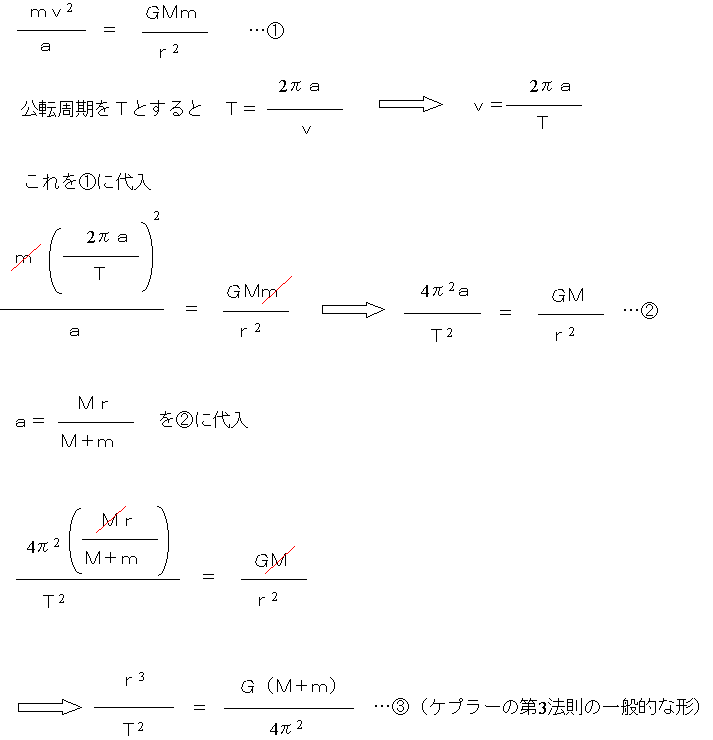
このように、天体間の距離の3乗と、公転周期の2乗の比は、二つの天体の質量の和に比例することがわかる。これにより、連星系の質量の和を求めることができる。詳しくはこちらを参照。
太陽の質量をM、惑星の質量をmとすると、太陽系ではM≫m(太陽の質量の方が圧倒的に大きい)なので、惑星の質量mを無視できる。すると上の式は右辺が一定となり、狭義のケプラーの第3法則が成り立つことがわかる。この式から、第1宇宙速度を求めることができる。

また逆に惑星の公転周期と太陽からの平均距離がわかれば、この式から太陽の質量M(惑星の質量を無視できるので)を求めることもできる。あるいは、惑星−(人工)衛星系においてこの式を利用すれば、(人工)衛星の質量は惑星の質量に対して無視できるので、惑星の質量を求めることができる。
第1宇宙速度:投げ出した物体が再び地表に落ちることはなく、その天体のまわりを回り出す最低の速度が第1宇宙速度であった。第1宇宙速度は人工衛星を打ち上げるときの最低の速さである。
いま、大気がない天体の地表すれすれを飛ぶ人工衛星を考える。つまり、天体の中心(重心)からの距離r、公転周期Tで天体のまわりを回っているとする。すると下のように、その人工衛星の速さが求まる。これが第1宇宙速度である。
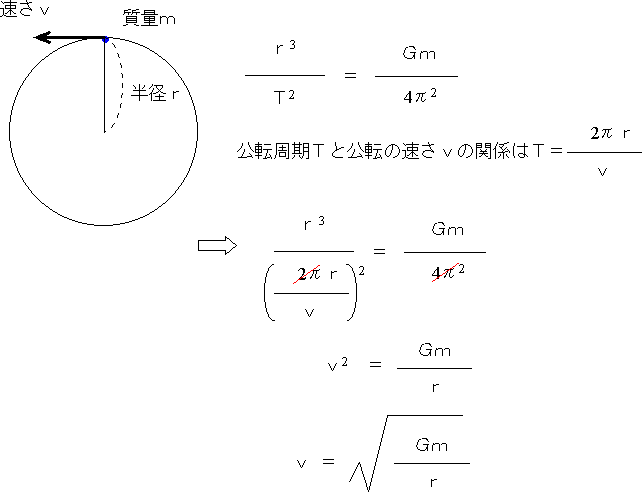
逆2乗則の発見:いま、質量mの物体が半径rの円周上を速さvで円運動をしている。

ケプラーの第3法則が成り立つように円運動をしているとき、向心力は質量に比例し、円運動の半径の2乗に反比例していることがわかる。こうして逆2乗則が導き出される。
リンゴと月:ニュートンはリンゴが落ちるのを見て、万有引力を発見したといわれている。もちろんその真偽はわからない。しかし、ニュートンはリンゴが落ちるという現象と、月が地球のまわりを回っているという現象は、本質的には同じ現象であるということを見抜いたことは間違いがない。
地球の表面(地球の中心=重心からの地球の半径分の距離)での重力加速度(g)の大きさは約9.8m・s-2という値である。
一方、地球と月の距離をr(m)とすると、月が地球の周りを27日(27×24×60×60秒)かけて回っているということから、その公転の速さは(月の軌道の長さ)÷(月の公転周期)だから2πr÷(27×24×60×60)(秒)。月の公転からわかる向心力の大きさは、月の質量をmとすると

つまり、地球の引力による地球表面(地球の中心から地球の半径の距離)での重力加速度の大きさは、月の位置(地球の半径の60倍の距離)でのそれより602倍大きいことを示している。これは地球の引力の大きさが、月の位置では地球の表面の1/602、つまり距離の2乗分の1になっていること、つまり万有引力は距離の2乗に反比例する力だということになる。
こうしてニュートンは、リンゴが(地球の中心に向かって)落ちる時に働く力と、月が地球の周りを回るときの向心力となる力は、結局は両方とも同じ地球の引力が原因で、その大きさが距離の2乗に反比例していることを確認したのだろう。
このページの参考になるサイト