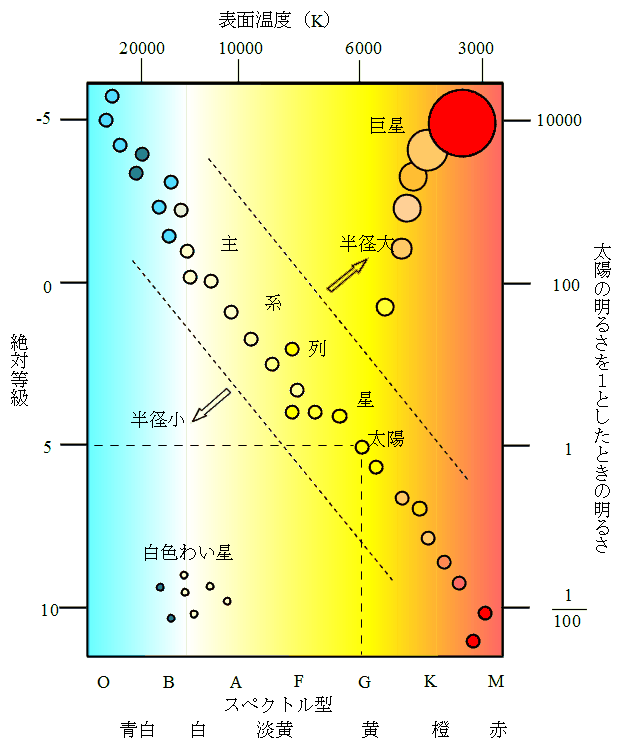
HR図
6. HR図
ヘルツシュプルング(1873年〜1967年、デンマーク)とラッセル(1877年〜1957年、アメリカ)は、縦軸に絶対等級、横軸にスペクトル型をとり、そこに恒星をプロットして恒星の研究を行った。この二人の名の頭文字をとり、このような図をHR図という。

HR図
縦軸は上ほど絶対等級が小さい、つまり明るいということを示す。横軸のスペクトル型は左からO、B、A、F、G、K、Mの順、つまり左ほど表面温度が高いことになる。縦軸の目盛りは絶対等級の他、光度(太陽の光度を1とすることが多い)でもよい。また、横軸の目盛りはスペクトル型の他、恒星の表面温度や色でもよい。
HR図は、恒星の性質や進化の研究に欠かせないものである。
太陽は絶対等級5、スペクトル型はG型の標準的(平均的)な恒星であることが、上のHR図からわかる。
また、HR図の中では、右上の恒星ほど半径が大きく、左下の恒星ほど半径が小さい。これについては下の巨星、白色わい星の項を参照。
なお、国立天文台岡山天体物理観測所の下のサイトでは、HR上の恒星のスペクトルを見ることができる。
http://www.oao.nao.ac.jp/stockroom/extra_content/story/ippan/hr/hr.htm
a.主系列星
HR図の左上から、右下に多くの恒星が並んでいる。これらを主系列星という。HR図の左ほど表面温度が高い、また上ほど明るい恒星であった。だから、主系列星は表面温度が高いほど明るい、逆に表面温度が低いほど暗いという、いわば当たり前の恒星である。太陽も主系列星の一員である。
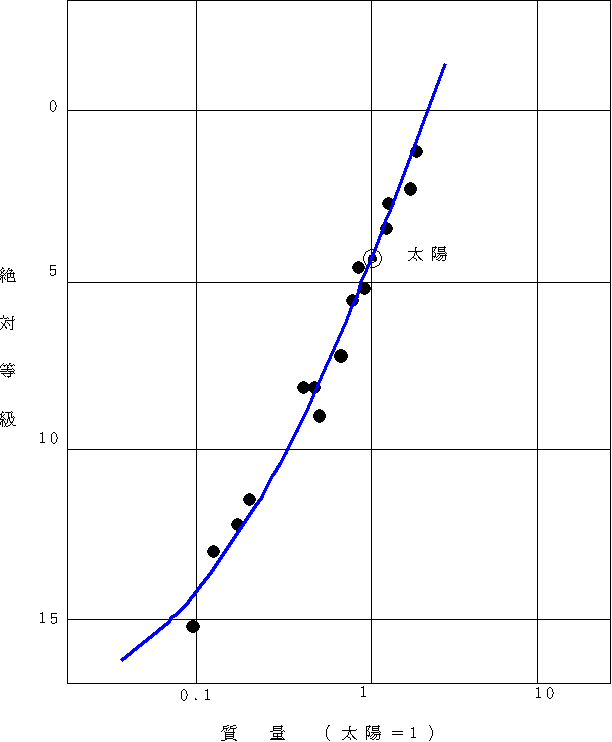
主系列星には、質量の大きな恒星ほど絶対等級が小さい(明るい)という関係がある。これを質量光度関係(光度は質量の3乗〜5乗に比例する)という。恒星の質量の求め方はこちらを参照。この質量光度関係は、質量を求めることができた恒星からわかった関係だが、逆にいったんこの質量光度関係が成り立つとすると、主系列星はこの関係を使って絶対等級から質量がわかることになる。こうして調べた恒星の質量は、だいたい太陽の10倍〜1/10の範囲に収まっている。
恒星の質量は、その恒星が持っている“燃料”の量である。だから、恒星の寿命は質量に比例する。また、光度はその燃料の消費の割合である。つまり恒星の寿命は光度に反比例する。
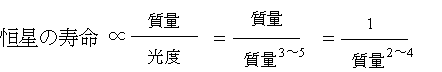
つまり、恒星の寿命は質量の2乗〜3乗に反比例することになる。いま、恒星の寿命が質量の3乗に反比例するとすると、太陽の2倍の質量の恒星は太陽の1/23=1/8の寿命しかないことになる。太陽の寿命は100億年程度と考えられているので、この恒星は12億年〜13億年の寿命ということになる。太陽の10倍の質量の恒星は太陽の1/103=1/1000、つまり1000万年の寿命しかないことになる。逆に太陽の1/2の質量の恒星は、太陽の8倍の800億年の寿命ということになる。
主系列星で質量が大きい恒星は、明るい恒星はO型やB型の恒星であり、これらの恒星の寿命は大変に短い。一方、M型の恒星は質量が小さい、つまり暗いので寿命は大変に長い。これらについてはこちらも参照。
b.巨星
HR図の右の上にも一群の恒星が分布する。HR図の右上の恒星は、表面温度が低いのにもかかわらず、絶対等級が小さい(明るい)というものである。表面温度が低ければ、一定の面積(単位面積、例えば1m2)から放射されるエネルギーは小さいはずである。だが、恒星が明るいということは、その恒星全体から放射される光の量は多いということになる。つまりその恒星は巨大(半径が大きい)ということがわかる。
これらの恒星を巨星という。赤い色をしたものが多いので、赤色巨星という場合もある。巨星の中でもとくに大きなものを超巨星ということもある。そのなかには太陽の半径の数百倍に達するものもある。
ただ、巨星といっても質量は太陽とそれほど変わらない。だから、太陽の半径の100倍の大きさの巨星は体積が1003の106(100万)倍にもなるので、逆に密度は太陽の10-6(100万分の1)しかないことになる。太陽の密度は1.4×103kg・m-3(1.4g/cm3)だから、約1.0×103kg・m-3(1.0g/cm3)とすると、巨星の密度は1.0×10-3kg・m-3(10-6g/cm3、1cm3が100万分の1g)ということになる。これは地球では高さ50km上空の空気の密度に相当する。真空に近いといってもいいくらいである。
太陽の半径は、6.96×105km、また太陽−地球間の距離は1.5×108kmである。だから太陽-地球の距離は、太陽の半径の約200倍(224倍)である。もし太陽が巨星になって、その半径がいまの200倍を超えたら、地球も太陽の中に飲み込まれてしまうことになる。巨星(超巨星)の中には、火星の軌道に達するようなもの(太陽の半径の330倍)もある。
c.白色わい星
HR図の左下にも一群の恒星が存在する。これらの恒星は、表面温度が高いのにもかかわらず、暗いということである。だから、b.巨星と同じように考えると、これらの恒星の半径は大変に小さいことがわかる。白色わい星の“わい(矮)”は小さいという意味である。
これらのことから、HR図で右上に位置する恒星ほど半径が大きく、左下に位置する恒星ほど半径が小さいことがわかる。つまり、HR図は恒星の半径も表わしていることになる。
白色わい星も、質量は太陽とそれほど変わらない。半径が太陽の1/100の白色わい星の体積は太陽の1/106(100万分の1)だから、密度は太陽の106(100万倍)の1.0×109kg・m-3(106g/cm3)、つまり1cm3が100万g=103kg=1ton、角砂糖程度の大きさのものが1ton(軽自動車並)ということになる。このような超高密度のものは、地球上ではまったく存在しない。ただ、このような超高密度のものでも、原子の構造(原子核とそのまわりを回る電子という構造)はまだ壊れていない。原子の構造までが壊れてつぶれたものが、パルサーであり、ブラックホールである。
こうした主系列星、巨星、白色わい星は、恒星の進化の段階を示していると考えられている。
表面温度と放射エネルギー:物体(厳密には黒体)が放射するエネルギーは、その物体の温度(絶対温度)の4乗に比例する。これをステファン・ボルツマンの法則という。放射エネルギーE(J)、物体の温度T(K)とすると、
E=σT4 ここでσ(シグマ)はステンファン・ボルツマン定数(5.67×10-8(J・s-1・m-2・K-4))
なお、J(ジュール)はエネルギーの単位である。別のエネルギーの単位であるcalとの換算は1cal=4.2J。ステファン・ボルツマンの法則についてはこちらも参照。
質量光度関係:恒星の表面重力は、恒星の質量(M)に比例して、半径(R)の2乗に反比例する。気体の温度は圧力(P)に比例して、密度に反比例する。密度は質量に比例し、半径の3乗に反比例する。圧力は単位面積にのしかかる重さである。これらから、圧力は質量の2乗に比例し、半径の4乗に反比例することがわかる。これらを総合すると、温度は質量に比例し、半径に反比例することになる。じつは、核融合反応を行っている恒星の中心部の温度は1000万Kくらいで、それほど違わないと考えられている。ということは、質量の大きな天体ほど半径が大きいということになる。質量と半径は比例している。実際主系列星ではそうなっている。
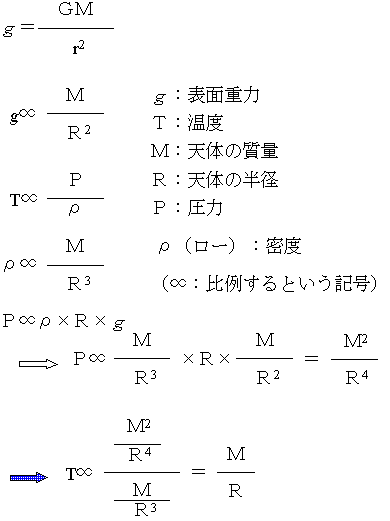
このことから、下のように恒星の密度が質量の2乗に反比例することもわかる。

だから質量があまり小さいと密度が高くなりすぎて、つまり気体(ガス)ではなくなり恒星になれない。木星(太陽質量の約1000分の1)の80倍以上ないと恒星にはなれないといわれている。一方あまり質量が大きすぎると、今度は密度が小さくなりすぎて不安定な状態になるので、これも恒星にはなれないという。結局恒星の質量は、太陽の10分の1〜10倍程度のものが多いことになる。
では、表面温度はどうだろう。あとは、中心部の熱がどのように表面に逃げ出てくるかである。恒星はガスの毛布をかぶっているので、その厚さと密度が熱の逃げやすさを決める。ガスの毛布が厚いほど熱は逃げにくいし、ガスの密度が高いほど逃げにくい。“保温効果”はこのように考えれば、ガスの密度×半径に比例する。また恒星の表面全体から出るエネルギーは表面積、つまり半径の2乗に比例すること、その半径は半径と質量が比例することから、恒星の明るさは質量の3乗に比例することがわかる。
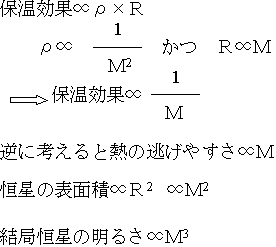
実際は、恒星を取り巻くガスの性質を考えるともう少し明るくなるので、上のかいたような質量光度関係となる。
恒星の半径:恒星の放射する光の量(L)は、単位面積が出すエネルギー(ステファン・ボルツマンの法則から求める)×その恒星の表面積だから、恒星の表面温度T(K)、半径r(m)とすると下の式で求めることができる。
L=σT4・4πr2
つまり、前半のσT4が単位面積から放射される光のエネルギー、後半の4πr2が恒星の表面積である。光のエネルギー(L)は観測からわかるし(厳密にはその恒星までの距離が必要)、その恒星の表面温度T(K)はスペクトル型(色)からわかるので、上の式から恒星の半径を求めることができるのである(平方根を開かなくてはならないが)。
いま、太陽の光度の1万倍の恒星(つまり絶対等級が-5等の恒星)の表面温度が4000Kだったとする。太陽の半径をrs、その恒星の半径をr、太陽の光度をLsとすると、太陽の表面温度は6000Kだから、
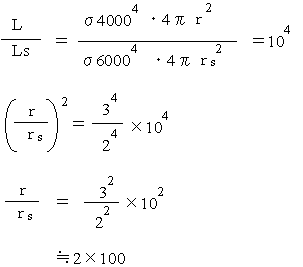
その恒星の半径は太陽の約200倍の巨星であることがわかる。