
| ���̃y�[�W�̖ڎ� | ||
| ��V�́@�F���̍\���i�R�j | ||
| �R�D�@��͌Q���璴��͒c�� | ||
| ���D��͌Q�A��͒c�A����͒c | ||
| ���D������͂܂ł̋����̋��ߕ� | ||
| �S�D�@�F���̉ʂĂ� | ||
| �p��ƕ⑫���� | ||
| �Q�l�ɂȂ�T�C�g | ||
�R�D�@��͌Q���璴��͒c��
�@�P�����O���[�v�����悤�ɁA��͂��O���[�v�����B�����̋�͌n������͂ł���召�̃}�[�������_�A����ɂ̓A���h�����_��͂Ȃ�30�ȏ�̋�͂ƂƂ��ɋǕ���͌Q�������Ă���i�Ǖ���͌Q���\�����Ă����͂̐��͗��ȔN�\2004�ɂ��j�B���̋Ǖ���͌Q�̂悤�ɁA3�ȏォ�琔�\�̋�͂����a150�����N���x�͈̔͂̂����܂��Ă��邪��͌Q�ł���B
�@���̋�͌Q���܂��W�܂��Ă���ɑ傫�ȊK�w�ł���A��͒c������B��͒c��50�ȏォ�琔��̋�͂���\������Ă��āA�傫����1000�����N���x�ł���B�����ɍł��߂���͒c�́A���a1200�����N�̂��Ƃߍ���͒c�ŁA����ꂩ��̋�����6000�����N����B
 |
 |
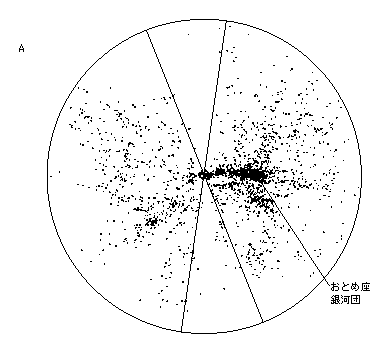
| �q�N�\���E�R���p�N�g��͌Q�B��������̋�͂������̈�ɖ��W���Ă���B | �������܍��̋�͒c�B�L����������Ă�����̂��ׂĂ���͂ł���B |
| �����V����@�V����y���Fhttp://www.nao.ac.jp/Gallery/index.html | |
�@�����Ă��̋�͌Q���͒c���܂��A�Ȃ肠���Ē���͒c������B����͒c��1�����N�ȏ�̑傫���������Ă���B�����̋�͌n�����Ƃߍ���͒c�ȂǂƂƂ��ɒ���͒c�������Ă���B������������͒c�����͂ދ�͂��قƂ�ǂȂ��̈�i�{�C�h�j�ƌĂԁB���̒���͒c�ƃ{�C�h�Ƃ����\���������F���ň�ԑ傫�ȍ\���ł���B
 |
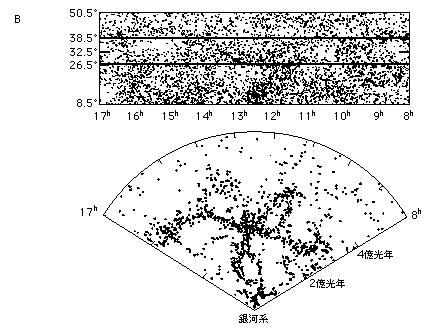 |
| �^����͌n�A�e�_����́B���Ƃߍ��𒆐S�Ƃ��钴��͒c�������Ă���B�i���ȔN�\2004�j | �A�Ȃ钴��͒c�Ƃ���Ɉ͂܂ꂽ�{�C�h�\����������.�~�̔��a�͖�7�����N�i���ȔN�\2004�j |
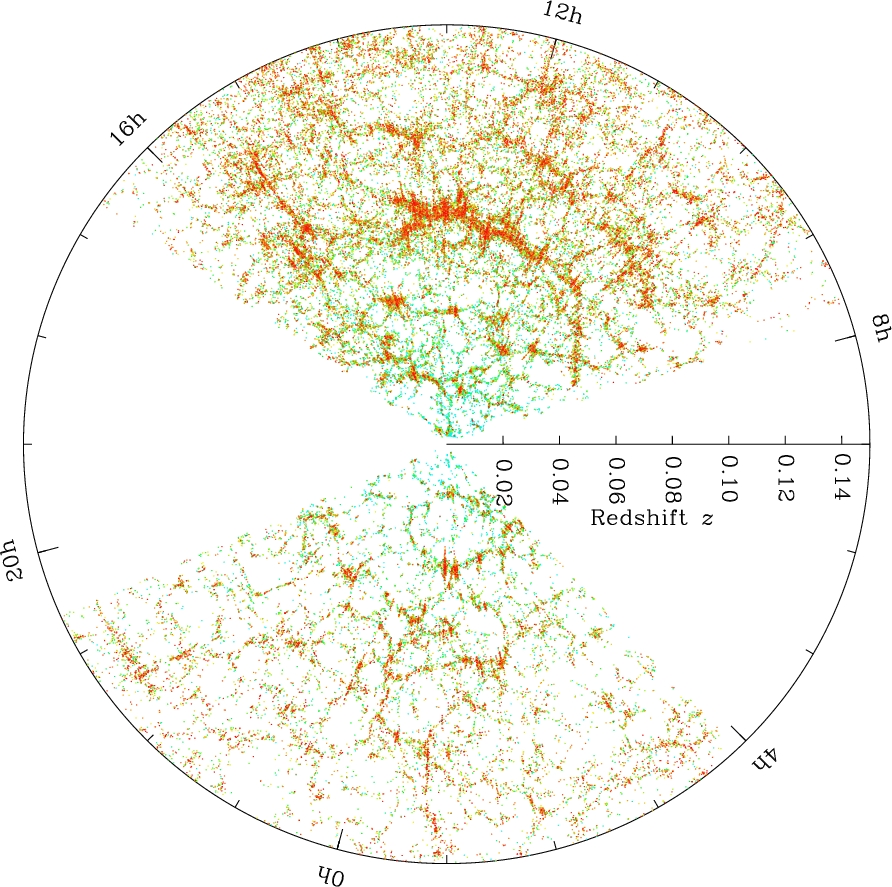
����ɉ����܂ŁA�܂��L���̈������B���S����͌n�A�O���͖�19�����N�B�X���[���E�f�W�^���E�X�J�C�E�T�[�x�C�B
http://sdss.physics.nyu.edu/pie/
�߂� ���̃y�[�W�̃g�b�v�� �@�ڎ��� home
�@��������������͒c�܂ł̋����͂ǂ�����̂��낤�B�߂���͒c�Ȃ�A���̒����P�t�F�C�h�ό����������āA�����ό��������x�W�����Γ��������߁A�������̓����Ɣ�r�������Ƃŋ��������߂�B����ɉ����A�P�t�F�C�h�ό����������ɂ����Ȃ�����A��͂̕��ς̖��邳�͐�Γ���-21�Ƃ������Ƃ𗘗p����B�܂�A��͒c�̒��Œ��Ԃ̖��邳�̋�͂͐�Γ�����-21���ƌ��Ȃ��āA�������̓����Ɣ�r�������Ƃɂ���ċ��������߂�̂ł���B�܂����V���̒��ŁA�^�C�vI�^�i�h���^�j�͂����Ƃ����邭�Ȃ����Ƃ��̖��邳�i��Γ����j���قڈ��ł���̂ŁA����𗘗p���āi�������̓����Ɣ�r���āj�A���������߂邱�Ƃ��ł���B����ȊO�ɂ�������͂����߂���@������A�����̕��@���g�����͂ł́A���ꂼ��̕��@�ŋ��߂������̔�r����(�N���X�`�F�b�N�j���ł���B
�@�����āA���炢�ɉ�����͒c�ł́A��ޑ��x�������ɔ�Ⴗ��Ƃ����n�b�u���̖@����p���ċ��������߂�̂ł���B��������������Q���B
�@�߂��P���܂ł̋������N�������A�������������ĔN������������ł��Ȃ��P�������������A�����Ɖ����P������̃X�y�N�g�����Ƃ�Ȃ��悤�ȋ�͂܂ł��ό��������x�W�Ƃ�����ɋ����̑�����@��ς���̂ł���B
�@�������������̑�����@�́A�����܂ł��N����������{�ł���B�܂����������̕��@���A�N�������̕��@�ŋ��߂���������킩����Γ������X�y�N�g���^�Ƃ̊W�i���Ȃ킿HR�}�j���A�N������������ł��Ȃ��قlj����P���ł����藧�Ƃ��Ă���B�����āA�P�t�F�C�h�ό������ό��������x�W���A�N�������╪���������狗�����킩��P���E���c�ł��̊W�����藧�̂ŁA�N�������╪������������ł��Ȃ��悤�ȉ�����͂̒��̃P�t�F�C�h�ό����ł����ꂪ���藧���낤�Ƃ���킯�ł���B����ɂ��̂悤�ȕ��@�ŋ��߂���������킩���́i�c�j�A���Ȃ킿�������̓��������Γ������킩����͂̕��ό��x��-21���Ƃ������ƂɂȂ�A�P�t�F�C�h�ό������������邱�Ƃ��ł��Ȃ��悤�ȉ�����͒c���A���̒��̋�͂̌������̓������狗���𐄒�ł��邱�ƂɂȂ�B���̂悤�ȕ��@�ʼn�����͒c�܂ł̋����𐄒肵�A���̋����ƌ�ޑ��x�̊W�i�n�b�u���@���j�����炩�ɂȂ����B���x�́A�����Ɖ�����͒c�A����ɂ��Z�C�t�@�[�g������N�G�[�T�[���A�n�b�u���̖@���ɏ]���āA���̋����ɔ�Ⴗ�鑬���ł���ꂩ�牓�������Ă���Ƃ��āA���������߂�̂ł���B�������ċ����̒i�K���ƂɁA�����̑�����@��ς��邱�Ƃ������̒�q�Ƃ����B
�@�N�������̑�����A���̏���������덷�����Ȃ肠��ƍl���Ȃ��Ă͂Ȃ�Ȃ��B�����Ă�������Ƃɐ���ɐ�����d�˂鉓���V�̂܂ł̋����ɂ͂����ψّ傫�Ȍ덷���܂܂�Ă���Ƃ������Ƃ���ɍl���Ȃ��Ă͂Ȃ�Ȃ��B�܂�A�F���̉ʂĂ܂ł̋�����A�F���̔N���̒l�͂܂��s�m�������傫���Ƃ������Ƃł���B
�߂� ���̃y�[�W�̃g�b�v�� �@�ڎ��� home
�S�D�@�F���̉ʂĂ�
�@�����̉F��������Ƃ������Ƃ́A�������B����܂ł̎��Ԃ��l����Ɛ̂̉F�������Ă���Ƃ������Ƃł���B���Ƃ��A1�����N�̔ޕ��̋�͒c���������������́A1���N�O�ɔ�����ꂽ�킯������A���̋�͒c��1���N�O�̎p�Ƃ������ƂɂȂ�B�����牓���̉F��������Ƃ������Ƃ́A�F���̗��j�����邱�Ƃł�����B
�@�����A�����̉F�����痈�����͑�ςɎア�B�t�ɂ����Ζ��邢�V�̂łȂ��ƌ����Ȃ��B���������ړI�ɓK������̂��A�Z�C�t�@�[�g��͂ł���A�N�G�[�T�[�ł���B
�@�Z�C�t�@�[�g����͔��Ɋ����I�ȋ�͂ŁA���̃G�l���M�[���͂悭�킩���Ă��Ȃ����A�������ƂƂ��ɁAX���A�ԊO���A�d�g�Ȃǂ��o����͂ł���B�Z�C�t�@�[�g���NGC4051������]�����ɂ���摜�͂������B
�@������N�G�[�T�[�͂����Ɩ��邢�B�����������N�͈̔͂����ʏ�̋�͂�100�{�ȏ�̋��������o���V�̂ł���B�����͈͂�������o���̂ŏ��P���I�V�̂Ƃ����Ӗ��ŏ����Ƃ����ꍇ������B��͂̒��S�j�Ŕ����I���ہi�d�̓G�l���M�[�̉���炵���B��͂̒��S�ɑ��݂��鋐��u���b�N�z�[���ɗ������ރK�X������~���~�Ղ���G�l���M�[�����o�����炵���B���N���z���ʒ��x�̃K�X���u���b�N�z�[���ɗ������߂A�ʏ��͂�100�{�Ƃ����G�l���M�[�������ł���j�������A��ςɋ��������o���B��������ɉ������̂�������B���݈���ԕ��Έ��iZ)���傫���N�G�[�T�[��Z��5���Ƃ����i���ȔN�\2004�A����]�����ɂ���摜�͂������j�B����͌�����95���قǂ̑����Ō�ނ��Ă���Ƃ������ƂɂȂ�B���ȔN�\2004���̗p���Ă���n�b�u���萔��75km�E��-1�EM����-1���g����3800Mpc�i124�����N�j�ޕ��̓V�̂Ƃ������ƂɂȂ�iM���������K�E�p�[�Z�N�Ɠǂ�100��pc�i�p�[�Z�N�j�A�܂�1pc��3.26���N�ł���j�B�܂�A124���N�O�̌��A124���N�O�̉F�������Ă��邱�ƂɂȂ�B������95���Ō�ނ��Ă���Ƃ������Ƃ́A�����Ō�ނ��Ă����F���̉ʂāi�F���̒n�����j�܂ł̋�����95���܂ł̂Ƃ��낪�������Ƃ������Ƃł�����B
���@�����V����̋���]�����g����h���g�����ϑ��`�[���́A128��8�疜���N�ޕ��̋�͂̊ϑ��ɐ��������B���ꂪ2009�N12��4�����݂Ŕ�������Ă���ʼn��̋�͂ł���B
�@�@�����V����A�X�g���g�s�b�N�X�i242�A2006�N9��15���j
�@���̂悤�ɉ����N�G�[�T�[����̌��͓r���̋�͒c�̎��ʂɂ��Ȃ����āi��͒c�̎��ʂ������Y�Ƃ��Ă͂��炢�āj�A��̃N�G�[�T�[����������Ɍ������肷�邱�Ƃ�����B���������d�̓����Y�ɂ��N�G�[�T�[�̂���]�����ɂ��ʐ^����������Q���B
�@�܂����̏͂́A����ꕔ-1-�@�F���̗��j���́���1�́@�r�b�O�o�����̏͂��Q�ƁB
�߂� ���̃y�[�W�̃g�b�v�� �@�ڎ��� home
��͒c�F���͋�͒c�̕\�i���ȔN�\2015���쐬�j�ł���B�Ȃ��A�Ԍo�A�Ԉ܂ɂ��Ă���������Q���B�܂��A�\���̌�ޑ��x�iV�j�͐ԕ��Έڂ��g���āA�M�҂����߂��B���̂Ƃ��A�ԕ��Έ�Z���傫���̂ŁAV�����~�i�i1+z�j2-1�j�j/�i�i1+���j2+1�j�Ƃ��������g�����BZ����������iZ<0.5���炢�Ȃ�j�AV����Z�ł悢�B���������͌����i3.0�~105km�Es-1�j�ł���B
| ���� | 2000 | �@ | ���� | ��͐� | �ԕ��Έ� | ���� | ��� ���x |
| �@ | �Ԍo | �Ԉ� | �@ | �@ | z | (�����N) | �i����/���j |
| �@ | h m | �� �� | �@ | �@ | �@ | �@ | �@ |
| ���Ƃߍ��c | 12 30.8 | +12 23 | 9.4 | 45 | 0.0039 | 0.59 | 1.17E+03 |
| ����c | 3 38.5 | -35 27 | 10.3 | �| | 0.0046 | 0.63 | 1.38E+03 |
| �|���v���c | 10 30.0 | -35 19 | 13.4 | 1 | 0.0087 | 1.2 | 2.60E+03 |
| �P���^�E���X���c | 12 48.9 | -41 18 | 13.2 | 33 | 0.011 | 1.5 | 3.28E+03 |
| ���݂ւэ��T�c | 10 36.9 | -27 31 | 12.7 | 50 | 0.0114 | 1.6 | 3.40E+03 |
| �����Ⴍ���U�c | 18 47.2 | -63 19 | 14.7 | 8 | 0.0139 | 1.9 | 4.14E+03 |
| ���ɍ��c | 8 20.6 | +21 04 | 13.4 | �| | 0.016 | 2.2 | 4.76E+03 |
| �y���Z�E�X���c | 3 18.6 | +41 30 | 12.5 | 88 | 0.0183 | 2.5 | 5.44E+03 |
| �| | 11 44.5 | +19 50 | 13.5 | 117 | 0.0215 | 3. | 6.38E+03 |
| ���݂̂����c | 12 59.8 | +27 58 | 13.5 | 106 | 0.0232 | 3.2 | 6.88E+03 |
| �| | 16 28.6 | +39 31 | 13.9 | 88 | 0.0309 | 4.2 | 9.13E+03 |
| �w���N���X���c | 16 5.2 | +17 44 | 13.8 | 87 | 0.0371 | 5.1 | 1.09E+04 |
| �| | 0 41.6 | -9 20 | 15.7 | 59 | 0.0518 | 7. | 1.51E+04 |
| ����ނ���c | 15 22.7 | +27 43 | 15.6 | 109 | 0.0721 | 9.1 | 2.09E+04 |
| �| | 10 58.3 | +56 46 | 17.0 | 74 | 0.136 | 17. | 3.80E+04 |
| �| | 4 54.3 | +2 56 | 17.4 | 186 | 0.203 | 25. | 5.48E+04 |
| �| | 2 39.8 | -1 35 | 17.8 | 40 | 0.373 | 41. | 9.20E+04 |
| Cl0024+1654 | 00 26.6 | +17 10 | �| | �| | 0.392 | 43. | 9.58E+04 |
| C10013+1609 | 00 18.6 | +16 27 | �| | �| | 0.55 | 54. | 1.24E+05 |
| MS1054-0321 | 10 57.0 | -03 37 | �| | �| | 0.82 | 70. | 1.61E+05 |
| RDCS J0910+5422 | 09 10.0 | +54 22 | �| | �| | 1.11 | 83. | 1.90E+05 |
| XMMXCS J2215 | 22 15.9 | -17 38 | �| | �| | 1.46 | 94. | 2.15E+05 |
| C1J1449+0856 | 14 49.2 | +08 56 | �| | �| | 2. | 106. | 2.40E+05 |
�@���̕\���g���āA�����ƌ�ޑ��x�̊W�i�n�b�u���̖@���j�����߂Ă݂�B���̂悤�ɋ����i�����N�j�ƌ�ޑ��x�ŁAMicrosoft Excel�̃O���t�쐬�@�\�ŃO���t������A�ߎ������̎��i�X�����n�b�u���萔�̒l�j��linest���ŋ��߂��B
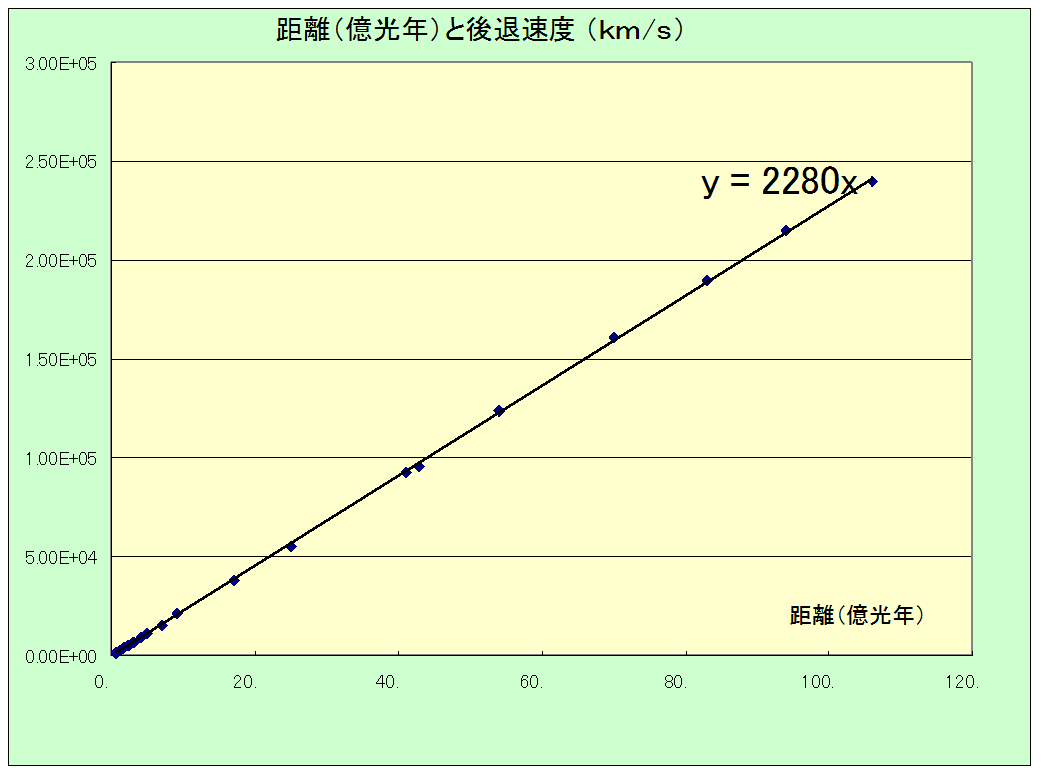
�@���ɂ��ꂢ�ɋ����ƌ�ޑ��x����Ⴕ�Ă��邱�Ƃ��킩��B���̒����̌X���i�n�b�u���̒萔�j��1�����N�ɂ�2280km�Es-1�ƂȂ�B���̒l�́A69.9km�E��-1�EM����-1�ł���B���ȔN�\2015�ł��n�b�u���̒萔�i���Ƃߍ��������Ƃ��āj�Ƃ���70km�E��-1�EM����-1�Ƃ��Ă��āA�قƂ�ǂ݂��ƂɈ�v����B����͓�����O�ŁA���ȔN�\�ł͐ԕ��Έڂ����ޑ��x�����߁A�u�F���_�v���狗�������߁A����炩��n�b�u���萔���o���Ă���B������A���ȔN�\�̐ԕ��҈ڂƌ�ޑ��x����n�b�u���萔���o���Ƃ������Ƃ́u�t�Z�v���Ă��邾���Ȃ̂ŁA��v����͓̂�����O�ł���B�Ȃ��AY�ؕЂ�0�Ƃ��ČX�������߂��2275�ikm�Es-1�E�����N-1�@�i74.2km�Es-1�EMpc-1�j�j�ƂȂ�B1Mpc��106pc�B
�߂� ���̃y�[�W�̃g�b�v�� �@�ڎ��� home
������͂܂ł̋����̋��ߕ��F��ɏ��������@�ȊO�ɂ��A�u��͂̉�]���x�Ƃ��̋�͂̐�Γ����͔�Ⴗ��v�Ƃ����o�����𗘗p��������ł���B�����A�����̕��@��6�����N���x�܂ł̋�����������Ȃ��Ƃ����B�����ł���ɉ�����͂ɂ��ẮA��͒c�ɂ���F���w�i�����i�R�j���ˁj���ω����邱�Ƃ�p���āi�F���w�i���˂̕ω��̓x�����͋�͒c���̓d�q�̉��x�▧�x�A��͒c�̑傫���ɔ�Ⴗ�邪�A��͒c���̓d�q�̉��x�▧�x�͂w���̊ϑ�����킩��̂ŁA�c��̋�͒c�̑傫�����킩��j�A���̋�͒c�̌������̑傫������A�O�p���ʂ̌����ŋt�ɋ��������߂邱�Ƃ��ł���B
�߂� ���̃y�[�W�̃g�b�v�� �@�ڎ��� home
�N�G�[�T�[�̖��邳�F�ŏ��ɔ������ꂽ�N�G�[�T�[��3C273�Ƃ������O�̃N�G�[�T�[�ł���B�ԕ��Έ�Z��0.158�Ȃ̂ŁA�����͒c�ł̎����g���Č�ޑ��x��4.4�~104m�Es-1�ƂȂ�B�n�b�u���̒萔70km�E��-1�EM����-1���̗p����ƁA���̃N�G�[�T�[�܂ł̋����́A550Mpc�i5.5�~108pc�A��18�����N�j�ɂȂ�B����A���̃N�G�[�T�[�̌������̖��邳��12.9�����ł���B�������̓����i���j�Ɛ�Γ����iM)�A�����i��pc�j�̊W�� ��-M��5log�i��/10�j ����Γ��������߂�ƁA�l��-25.8�i��-26�j�ƂȂ�B����͂ӂ��̋�̖͂��邳-21���5�����������A�܂�100�{���邢�Ƃ������Ƃ��킩��B
�߂� ���̃y�[�W�̃g�b�v�� �@�ڎ��� home
�F���q���J���@�\�́u�I�����C���E�X�y�[�X�m�[�g�v�Fhttp://spaceinfo.jaxa.jp/note/note_j.html
�߂� ���̃y�[�W�̃g�b�v�� �ڎ��� home