| このページの目次 | ||
| 第1章 天体(惑星)としての地球 | ||
| 1. 地球の運動 | ||
| 2. 地球の自転の証拠 | ||
| a.フーコーの振り子 | ||
| b.コリオリの力(転向力) | ||
| c.赤道における自転の証拠 | ||
| 3. 地球の公転の証拠 | ||
| a.年周視差 | ||
| b.年周光行差 | ||
| 用語と補足説明 | ||
| 参考になるサイト | ||
1. 地球の運動
地球は自転しながら、太陽のまわりを公転している。自転は地球の回転運動で、地軸(北極と南極を結ぶ軸)を軸として、1日に1回転している。公転は太陽のまわりの回転である。地球は1年かけて太陽のまわりを回っている。1日や1年の長さについてはこちらを参照。
地球の自転により、太陽・月・惑星・恒星は東から昇り、西に沈むように見える。こうした1日での天体のみかけの動きを日周運動という。
地球の公転により、季節により見える恒星(星座)が異なったり、季節の変化が起こる。
2. 地球の自転の証拠
動いているはずの地球に乗っているのに、動いているという実感はない。日常生活では地球が自転しているという証拠を得ることはなかなか難しい。ここではーコーの振り子とコリオリの力を挙げる。
a.フーコーの振り子
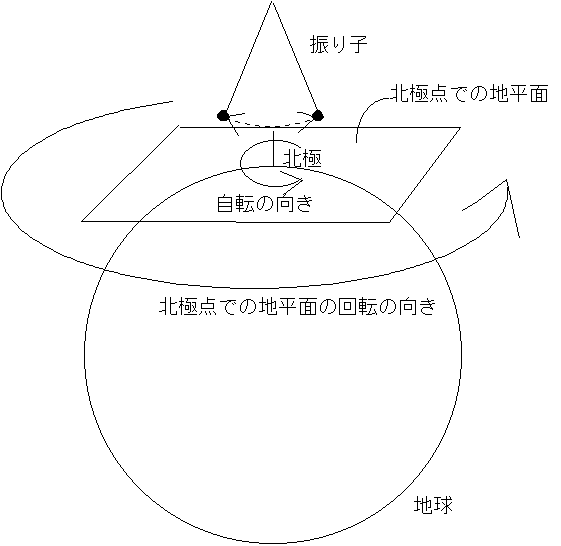
フーコーの振り子の原理は簡単である。例えば、下図のように北極点で振り子を振ってみる。この振り子には地球の重力しか働いていない。つまり振動面を変えようとする力ははたらいていない。だから宇宙から見れば、振り子の振動面は変わらず、その下の地球が回転しているだけである。

このとき、宇宙から見れば振り子の振動面は変わらないのだが、下の地球の上の振動方向の目印を考えると、初めA-B方向に振動していたのに、その下の地球が回転しているため、だんだんとC'-D'方向に振動する方向が変わっていることになる。地球上(北極上)でこれを見ると、自分が動いていること(地球が回転していること)はわからないので、初めA-B間で振れていた振動面が、いつのまにかC-D間(C'-D'間)で振れるように振動面が回転するようになる。つまり、北極(南極)では、1日に振り子の振動面が1回転することになる。
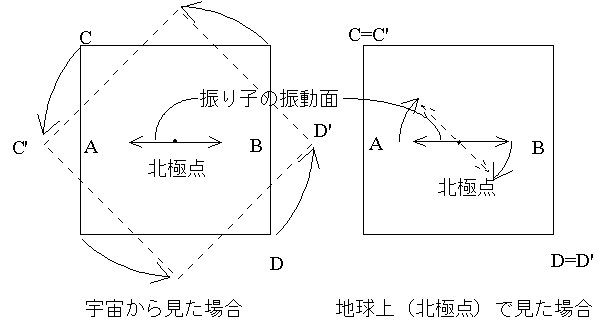
北極・南極以外ではちょっと難しいが、緯度が高いほど1日の回転角は大きく(360°に近く)なり、緯度が低いほど1日の回転角は小さくなる。赤道上ではまったく回転しない。詳しくは下を参照。
フランスの物理学者フーコー(1819年〜1868年)は、1851年にパリのパンテオン宮殿で、長さ67m、おもりの質量27kgという振り子を用いてこの実験を行い、地球の自転を確かめた(下図)。逆にいうと、1851年までは地球の自転の証拠はなかったということになる。実際には、振り子の支点の摩擦などのために、短い振り子やおもりの質量が小さい振り子ではすぐに減衰してしまうので、振動面の回転がわかるほどの長い時間、振り子を振らせることは難しい。科学系の博物館などにある、フーコーの振り子の実物を見てみよう。動いているフーコーの振り子を見られる施設の一覧については、大阪市立科学館学芸員の渡部義弥氏の調査がある。その結果はこちら。

通信総合研究所:http://www2.crl.go.jp/kk/e414/2003ippan/setsumei/fu-ko-.doc
(通信総合研究所が情報通信研究機構(NiCT)に組織が統合されたため2006年1月6日現在リンク切れ)
b. コリオリの力(転向力)
地球の自転のもう一つの証拠は、地球では運動している物体に対してコリオリの力(転向力)というものが働いて、北半球では運動している物体が進行方向に対して右へ右へと曲げられていく(南半球では左へ左へと曲げられていく)という現象である。これも、理解が少し難しい。
いまV2という速度(速さと向きを考えた量)で動いている電車の中から、電車に対してV1という速さでボールを投げる(本当にやってはいけない)。ここでは簡単にするために、電車の速度に対して直角方向に投げているが、本当はどの向きにボールを投げても、V1とV2が作る平行四辺形の対角線の向きに斜めに飛んでいく(地上から見た場合)。これは力の平行四辺形と同じである。
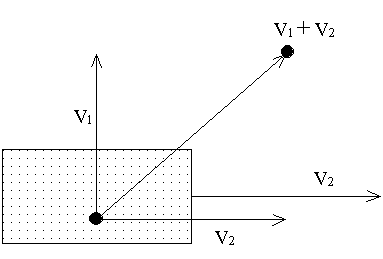
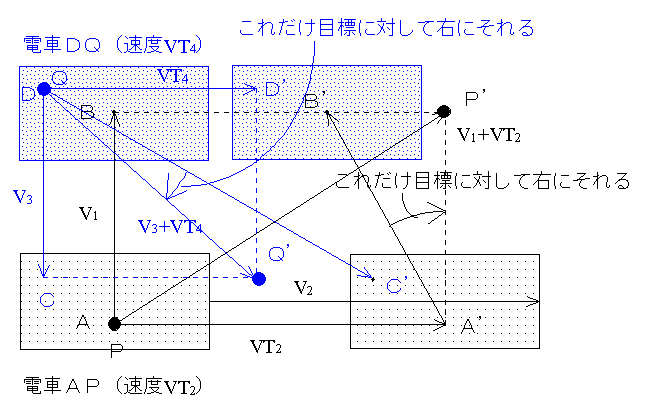
ここで、平行して同じ向きに同じ速さで等速直線運動をしている2台の電車を考える。下図の下の電車の速度VT2>上の電車の速度VT4とする。いま、下の電車のAから上の電車のBに向けてボールPを投げる。ボールはつねにAの真ん前を飛んでいき、ある時間後にはP’に到達する。しかし、目標であったBはまだB’の位置にまでしか来ていない。ここで、電車の姿やまわりの景色はまったく見えず、電車が動いているときの振動もなく、目標のBだけしか見えないとすると、ボールPを投げた人にとっては、なぜか目標であるB(B’に移動している)にボールが当たらず、ボールは目標の右に自然にそれてしまったように思えるだろう。
逆に、上の電車Dから下の電車Cに向かってボールを投げても、Dにいる人にとってはボールは目標であるC(C’に移動している)には当たらず、同じように目標に対して右にそれることがわかる。
地球を下の図のような円盤として考える。地球の自転による回転の距離の大きさ(つまり速さ)は赤道で最大、北極に向かってだんだん小さくなり、北極で最小(0)になる。だから上の図のように、赤道から北極向かってボールを投げようが、北極から赤道に向かってボールを投げようが、いずれにしても目標に向かってまっすぐには飛んでいかず、なぜか右へ右へと曲がっていってしまうことになる。
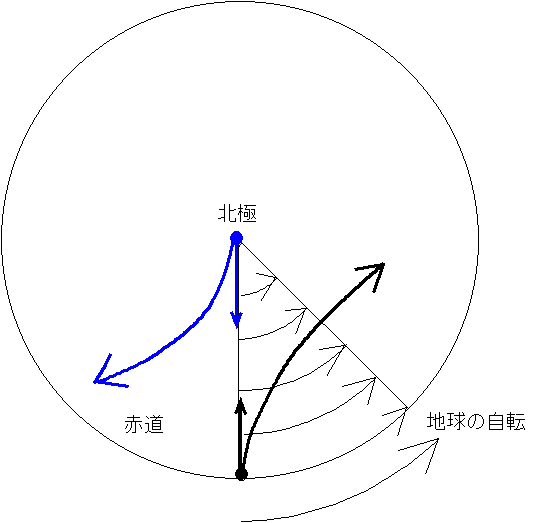
このように、回転している地球の上では、物体の進行方向を曲げようとする力が働いているように見えるので、これをコリオリの力(転向力)という。でも、これは“本当の力”ではなく、どのような立場で運動を見ているか、その立場の違いで生ずる“見かけの力”なのである。ここではそれについては深入りしない。コリオリの力の大きさの見積もりは下を参照。
コリオリ:フランスの物理学者(1792年〜1843年)。
ともかく、実際地球上で、例えば運動場でボールを思いっきり投げても、そのボールが必ずすべて右へ右へと曲げられていくことはない。もし、日常生活でもコリオリの力の影響が見えるなら、古代の人も地球の自転に気が付いていただろう。コリオリの力は、気象現象(高気圧・低気圧の風など)の大規模なスケールでないと、その影響が見えてこないのである。
低気圧の渦が、北半球では必ず左巻き、南半球では必ず右巻きになるのは、コリオリの力のせいである。これは今日では、気象衛星の写真を見ると一目瞭然であり、これこそが地球の自転の証拠なのである。高気圧・低気圧などの風の吹き方はこちらを参照。どのような場合にコリオリの力の影響が現れて、どのような場合は無視できるかは下を参照。
c. 赤道における自転の証拠
フーコーの振り子が1日に回転する角度もコリオリの力の大きさも、緯度のサインに比例する。つまり、赤道(緯度0°、sin0°=0)では、フーコーの振り子の振動面も回転しないし、コリオリの力も現れない。では、赤道での自転の証拠にはどのようなものがあるのだろう。
c-1 日周光行差
地球が自転しているということは、赤道では24時間(86400s)で40000km動いているということである、つまり0.46km・s-1(460m・s-1)という速さで動いている。これは、地球の公転の速さ、30km・s-1の1/65(65分の1)でしかないが、それでも年周光行差と同じように、恒星の見かけの向きが自転の向きに少し傾く(0.32″傾く)。こうして、恒星の見かけ上の位置が、1日を周期として変化する。これが日周光行差であり、自転の証拠となる。もちろん、赤道でなくても日周光行差はあるが、緯度が高くなるその値は小さくなる(緯度のコサインに比例する)。
c−2 エトベス効果
赤道で自転と同じ向きのま東に向かって動くということは、自転の速さにそれが加わるということである。つまりそれだけ遠心力が増して、見かけ上重力が小さくなる(ので、体重が軽くなる)。ま西に動けば逆である。
例えば、時速100km(秒速28m)でま東に動くと、体重は0.04%程度軽くなる(体重50kgの人だと.002kg(20g)ほど軽くなる。ま西に時速100km(秒速28m)で動けば逆に、体重は0.04%程度重くなる(体重50kgの人だと0.02kg(20g)ほど重くなる。こうした東西方向の動きによって、違いが生ずることが、自転の証拠となる。赤道で幅跳びとかやり投げをするときには、東に向かって跳んだり、投げたりする方が有利であることがわかる。赤道上で東向きに時速800kmで移動しているジェット機に乗ると、乗るだけで160gくらいのダイエット?
こうしたた効果を、発見者の名前をエトベス効果という。エトベス効果も日周光行差と同じように、赤道で最大で、緯度が高くなると小さくなる(緯度のコサインに比例する)。
エトベス効果は、地面に対して垂直な向きに現れるコリオリの力と考えてよい。
※ エトベス(エトヴェシュ)は1848年〜1912年、ハンガリーの物理学者。
3. 地球の公転の証拠
a.年周視差
地球−太陽の距離が1.5×108kmなので、地球は半年後には3.0×108km離れた地点に位置することになる。だからこのときに視差を生ずる。この視差の1/2を年周視差という。図では、∠E1SOや∠E3S1Oなどがそれである。S1のように公転面に対し太陽の真上(?、Sの位置)に位置しない恒星でも、その恒星(S1)と太陽(O)結んだ線に対して垂直な地球の軌道の直径(半径E3O)を考えて、その端の地球を考えればよい。1
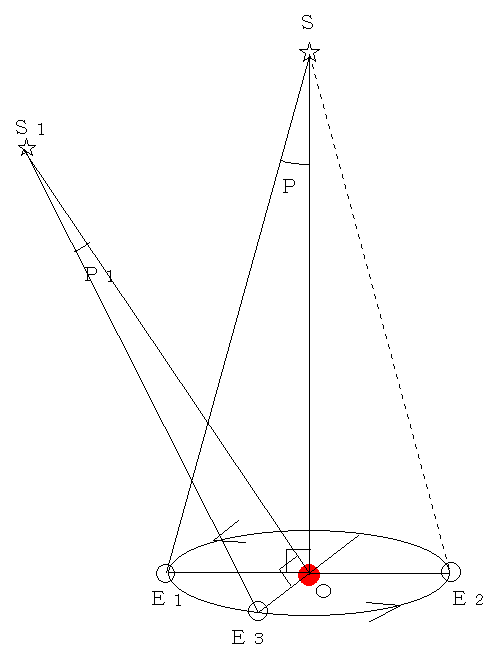
こうして、天球上で恒星はその位置により、1年を周期とする円−だ円-直線を描くはずである。
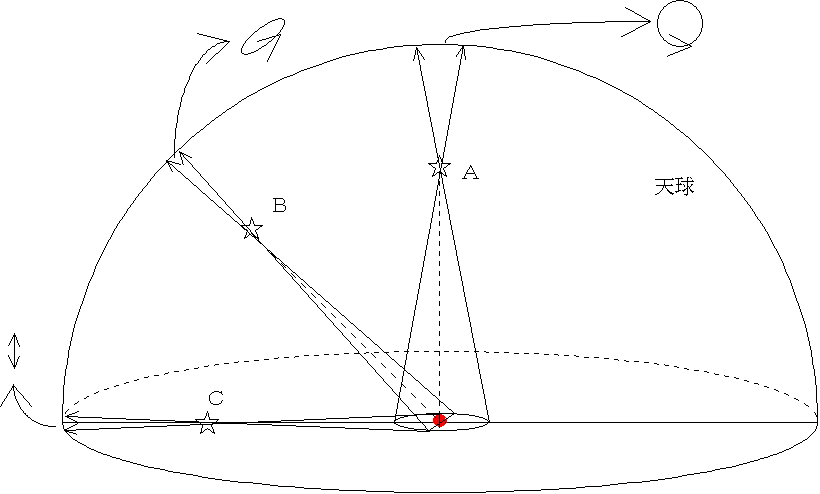
だが、実際にはこの年周視差非常に小さい。すなわち恒星までは大変に遠い。われわれに最も近い恒星ケンタウルス座α星でもその角度は0.742″(3.6×10-5rad、1°の約1/5000の大きさ)でしかない。ついで、バーナード星の0.549″(2.7×10-6rad)。それ以外はみな0.5″未満である。全天で一番明るく見えるシリウスの年周視差は0.379″(1.8×10-6rad)で、7番目の大きさ(近さ)になる。
昔は、恒星はもっと近いだろうと思われていた。だが、史上最高の肉眼観測者チコ・ブラーエ(1546年〜1601年)ですら、この年周視差を測定できなかった。実証的なチコはこのことをもって、地球が太陽のまわりを回っている考え(地動説)を否定したのだ。つまり、もう一つの可能性=年周視差は観測できないほど小さい(恒星までの距離は大変に遠い)ということまでに思いを巡らせることができなかった。当時の「常識」からすればやむを得なかったであろう。
年周視差が最大のケンタウルス座α星の視差0.742″(3.6×10-6rad)は、0.36mmの大きさ(直径)のものを1km離れた見たとき大きさ(見かけの大きさ)である。いくら目のいい観測者でも、そのようなものが見えるはずはない。
年周視差の測定に最初に成功したのは、望遠鏡が天体観測に使われるようになってからでもかなり後になった1838年のことであり、ベッセルが白鳥座61伴星について0.29″(0.286″、1.4×10-6rad)を求めた。
なお、年周視差が測定できたということは、その恒星までの距離を求めることができるということである。これについてはこちらを参照。
※ 年周視差は理科年表2003年版(国立天文台、丸善)の値を使っている。
b.年周光行差
風のない日に雨が降っている。そのとき、傘はまっすぐ上に向けて差せばよい。しかし歩き出すと、傘を少し進行方向に向けて差した方がいい。あるいは、電車の窓から雨を見る。電車が動いていないときはまっすぐに落ちてくる雨も、電車が動き出すと進行方向前から斜めに落ちてくるように見える。
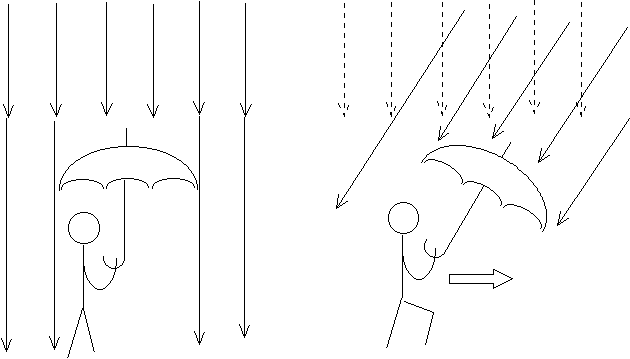
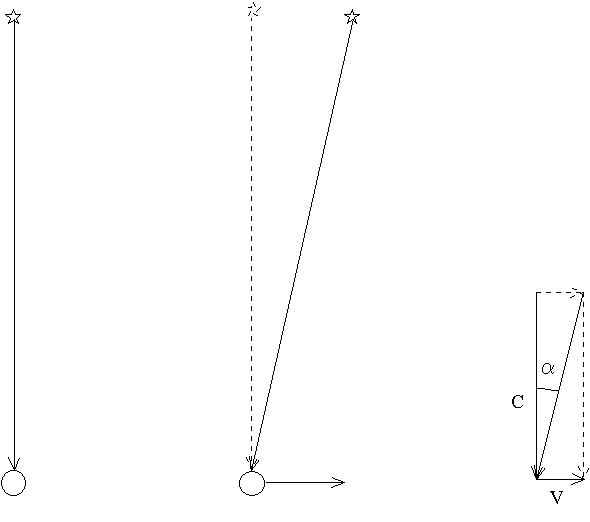
恒星からの光も同じである。地球が光速に対して無視できない速さで動いているために、恒星からの光も地球の進行方向斜め前から来るように見える。これも、年周視差と同じように1年を周期として向きを変える。これを年周光行差という。
年周光行差の大きさ、つまり地球が動いていないときにやってくるはずの光の向きと、地球が動いているためにやってくる光の向きのなす角度(α)は、恒星からの光がやってくる向きと地球の進行の向きがちょうと90°になるときに最大となる。そのとき、光速をC、地球の公転の速さをVとすると、
tanα=V/C となる。
となる。
この角度αは、1728年にブラッドレーによって測定され、値は20.5″であった。つまり、年周視差の最大の値よりも30倍近くも大きい。だから、年周視差の測定をさかのぼること100年以上も前に測定できたのだ。この年周光行差が、地球が動いていることの(地動説の)最初の証拠になった。ニュートンの死後1年後のことである。
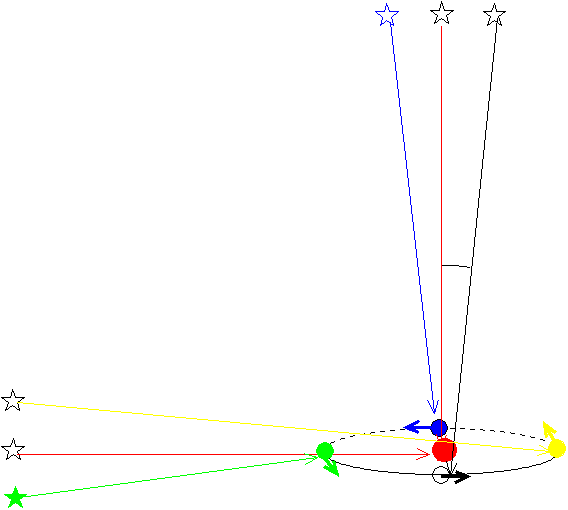
年周光行差による、天空上の恒星の動きも年周視差と同じように、その恒星の位置により円−だ円-直線となる。だがその大きさは年周視差と異なり、その恒星までの距離によらず、ただ太陽系に対する位置だけで決まる。黒い地球の位置では、太陽の真上の恒星から光が黒い線の向きからやってくるように見える。青い地球の位置では青い線の向きになる。以下、黄色は黄色、緑色は緑色に対応している。
年周光行差の最大値(20.5″)が求まれば、地球の公転の速さから光速を求めることができる。昔、光速はこのような天文現象を利用して求められていた。他に、木星の衛星の食から光速を求める方法もある。
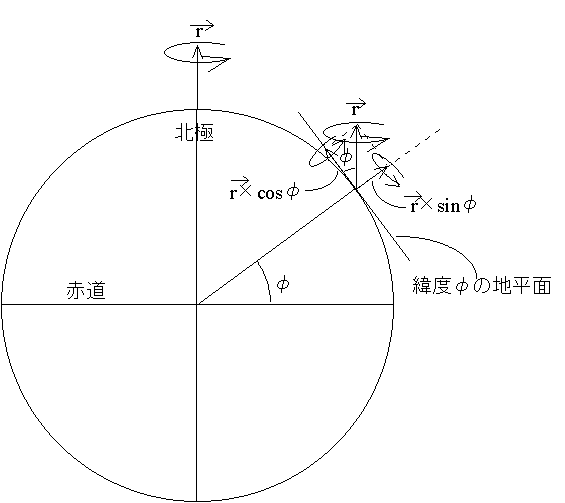
フーコーの振り子:フーコーの振り子の振動面が、任意の緯度のおいて1日に何度回転するかの説明は難しい。ある緯度においては、自転のよる回転軸はその緯度での地平面に対して垂直ではない。回転も力と同じように合成・分解できる。だから、回転もベクトルと考えて、緯度φ(ファイ)における地球の回転ベクトルは、下図のようにその地平面に垂直な成分(大きさはr×sinφ)と、水平な成分(大きさはr×cosφ)にわけることができる。振り子の振動面の回転に関係するのは、地平面に対して垂直な成分のみである。その大きさがr×sinφということは、フーコーの振り子の振動面の回転の大きさも、1日に360°×sinφとなる。
実際に数値を当てはめてみる。緯度90°(北極と南極)ではsin90°=1だから、フーコーの振り子の振動面の1日の回転量は360°。赤道ではsin0°=0なので、フーコーの振り子の振動面は回転しないことになる。緯度30°では、sin30°=0.5なので、180°。東京は北緯35°、sin35°=0.5736なので、フーコーの振り子の振動面は1日に360°×0.5736=206.5°回転することになる。
sin(サイン)、cos(コサイン)についてはこちらを参照。
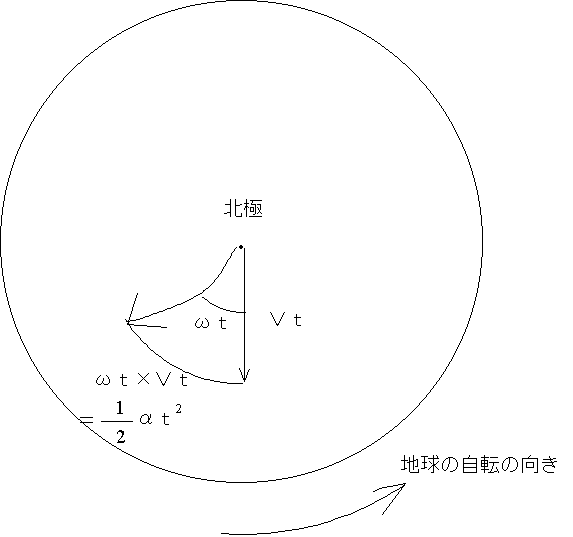
コリオリの力の大きさ:いま地球を円盤と考えて、北極からV(m・s-1)という速さでボールを投げる。t秒後にはVt(m)だけ移動する。地球の自転の角速度をω(rad・s-1)とすると、コリオリの力によるずれの量は、半径Vt(m)、中心角ωtの弧の長さVt・ωtになる。ここでコリオリの力による加速度をαとすると、加速度αによるt秒間の移動量は1/2αt2である。だから、1/2αt2=Vt・ωt。つまり、α=2ωVとなり、加速度は回転の角速度と、物体の速さの積に比例していることがわかる。
質量mの物体が、速度Vで運動しているときの、コリオリの力(f)はf=2mVωとなる。さらに緯度φの水平面においては、地球の自転の角速度はωsinφとしてよいから(上参照)、地球上でのコリオリの力はf=2mVωsinφとなる。
なお、角度の単位ラジアン(rad)についてはこちらを参照。
コリオリの力とその影響:上の例で実際の数字を入れてみる。地球の自転は1日で360°(2π(rad))なので、1秒では4.2×10-3°(7.27×10-5rad・s-1)。ここで、北極から時速100km(28m・s-1)のボールを投げる。そのボールはピッチャー・プレートとホームベースの距離18mを0.64秒で通過する。この間に地球は4.2×10-3°・s-1×0.64s回転する。だからずれの量は半径18mの円周の4.2×10-3°・s-1×0.64s/360°ということになる。
2π×18m×4.2×10-3°・s-1×0.64s/360°=8.4×10-4m(0.84mm)。
つまり、ホームベース上でのずれは、わずかに0.84mm。緯度の低い日本付近でのずれは、コリオリの力が小さくなるので、さらに小さくなり約0.4mm程度でしかない(8.4mm×sin35°)。どのようにコントロールの優れたピッチャーでも、このような精度を持って投げることのできる人などいない。それよりも、ボールの回転や風の影響の方が強いだろう。だからボールを投げるなどの日常生活においては、コリオリの力を無視できるのだ。無視できなければ、上に書いたように古代の人だって、コリオリの力に気がついていただろう。
別な見方をしてみる。ものを投げた後、その物体にはコリオリの力しかはたらかないとする(重力や空気の抵抗はないとする)。すると、その物体の進行方向に向かって直角に右へ右へはたらく力がつねにはたらくことになる。だから、最終的にはその物体は円を描いてもとに戻るであろう。つまりコリオリの力が向心力(円運動を起こす力、例えば太陽の引力が向心力としてはたらくので、地球は太陽のまわりを回っている)としてはたらいたことになる。
半径rの円周を、質量m、速度Vで円運動行う物体にはたらく向心力fは、f=mV2/r。この向心力は、ここではコリオリの力だから緯度φにおいては、上の結果を使って
2mVωsinφ=mV2/r
コリオリの力によってできる円運動の半径は、r=V/(2ωsinφ)となる。このrの大きさと、考えている現象のスケールを比較すればよい。緯度φを決めれば、地球の自転の角速度は7.27×10-5rad・s-1という一定の値だから、rは運動している物体の速度に比例することになる。だから、速度1m・s-1(秒速1m)の物体がつくり円運動の半径rだけを求める。東京付近の緯度35°とすると、sin35°=0.57。
r=1m・s-1/(2・7.27×10-5rad・s-1・0.57)=1.2×104m(12km) … (1)
上の例で考えた投手が投げるボールの速さは28m・s-1だったから、(1)の28倍、すなわち366km。直径にすれば670kmにもなる。これは東京−神戸間を楽に上回る距離である。つまり670kmに対する野球場の最大の長さを120m(0.12km)比べれば、この120mという範囲では、半径370kmもの円周の一部がその中にあっても曲がっているということはわからないだろう(直線にしか見えないだろう)。
あるいは、秒速0.1m(秒速10cm)で排水口に吸い込まれる水が作る渦巻きも同じように考えると、(1)の0.1倍の半径1.2kmの円になる。まさか、各家庭でこの大きさ(直径2.4kkm)に対して無視できないほどの大きさの洗面所・あるいは浴槽があるとは思えない。
このように考え・計算していけば、日常生活の範囲内では、コリオリの力の影響は現れないということが理解できる。
一方、風速5m(5m・s-1)の風が吹くという現象を考える。この風の作る渦巻きの半径は(1)の12kmの5倍の60km。これは関東平野にすっぽりと収まる大きさである。だから、気象現象みたいに大きなスケールでの現象の時には、コリオリの力の影響がはっきりと現れるのである。実際に北半球での低気圧性の渦(中心に吸い込まれる渦)は、必ず左巻きになる。
 |
左の画像をクリックすると動画が再生されます。
赤道を挟んだ両側で渦の巻き方が逆なり、また赤道では渦ができないことを示します。残念ながら根本的に間違っていて、もしコリオリの力で渦の巻き方が決まるのなら北半球では左巻きの渦になるはずなのに、演示者は右まきの渦をつくってしまっています。そもそも、上に書いたようにコリオリの力は洗面器程度の大きさ(スケール)ではその影響は出ません。またさらに、コリオリの力はその土地の緯度のサイン(sin)に比例するので、緯度0°である赤道(付近)ではコリオリの力はゼロです。これは巧妙な手品です。 ※ 2013年12月、ケニアを旅行中、赤道の町ナニュキで「赤道商売」(赤道を挟んだ南北で渦の巻き方が逆なり、赤道では渦ができないことを示す商売)が実在した。ビデオで撮影してyoutubeにアップした。 |
 |
左の画像をクリックすると動画が再生されます。
東京都調布市の古刹深大寺の水路で見られた右巻きの渦です。このような小さな現象の場合は、コリオリの力は効いてこないので、他の要因で渦の向きが決まります。たからこのように右巻きになる場合もあります。 |
 |
左の画像クリックすると動画が再生されます。
南半球ヨハネスブルグ近郊のホテルの洗面所の排水口にできる渦です。左巻きも右巻きもできることがわかります。つまり、この程度のスケールではコリオリの力は効いてきません。 ※ 2018年7月14日、南アフリカ共和国ヨハネスブルグ近郊のホテルで撮影。 |
エトベス効果:いま、赤道上をvという速さでま東に動くとする。その角速度は、地球の半径をRとすると、v/R(rad・s-1)である。だから遠心力はR(ω+v/R)2となる。ここでωは地球の自転の角速度で7.3×10-5rad・s-1(=2πrad÷(24×60×60s))。遠心力はその分、重力が小さくなる。その大きさは、単位質量(1kg)にはたらく遠心力はR・ω2だから、静止している場合と較べて
R・ω2−R2(ω+v/R)2=R・(ω2−(ω2+2・ω・v/R+(v/R)2))≒−2ωv ((v/R)2の値は小さいとして省略)
これが、赤道でま東(あるいはま西)に動く場合のエトベス効果による重力の補正値となる。静止しているときの重力加速度をg、vという速さでま東に向かって動いているときの(みかけの)重力加速度をg'とすると、g'=g−2ωvだからg'/g=(g−2ωv)/g=1−(2ωv)/g。g≒10(m・s-2)だから、0.2ωvだけ重力が小さくなる。
例えば、時速100km(秒速28m)では、0.2×7.3×10-5×28=0.0004(0.04%)。
一般に、緯度φ、方位角(真北から何度東西に向いているか)αとすると、補正値は2ωcosφ・sinαとなる。sin(サイン)、cos(コサイン)はこちらを参照。
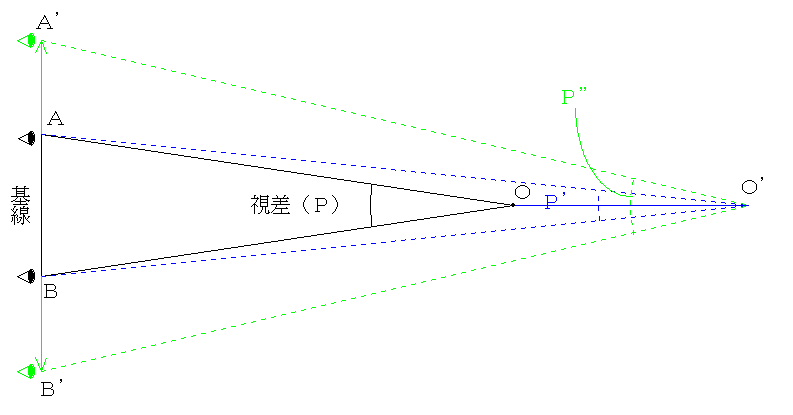
視差:離れた2地点からあるものを見ると、見える向きが異なる。そのとき、2地点の距離を基線(A-B)といい、見える向きの差(P)を視差という。ヒトの目も二つあるので視差を生じ、ものまでの距離をつかむこと、つまり立体視ができる。
基線の長さが同じなら距離が遠くなると視差は小さくなり、距離が同じなら基線の長さを長くとれば視差が大きくなる。
年周光行差から光速を求める:年周光行差α、光速Ckm・s-1,地球の公転の速さVkm・s-1とすると、上のように
tanα=V/C
ここで、地球の公転の速さを求める。地球の軌道を円とすると、軌道半径は1.5×108kmだから、その軌道の長さは2π×1.5=3.0π×108kmとなる。この距離を1年で移動する。1年=3.16×107秒だが、約π×107秒sとする。すると地球の公転の速さVkm・s-1=(3.0π×108km)÷(π×107s)=3.0×10km・s-1(30km/秒)となる。
一方、20.5″=9.9×-5rad(1″=4.85×10-6rad)なので、tan20.5″=tan(9.9×-5rad)=9.9×10-5
※ 角度ラジアン(rad)と三角関数についてはこちらを参照。
つまり、9.9×10-5=3.0×10km・s-1÷C
これから C=3.0×105km・s-1(秒速30万km)が求まる。