(1) 力の表し方
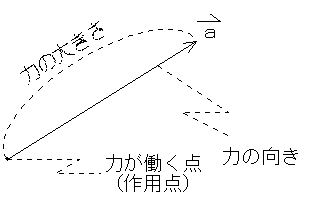
力は大きさだけでなく、向きも持っている。だから矢印(ベクトル)で表わすと便利である。矢の長さで力の大きさを、矢の向きで力の向き表わす。下の図の矢印aで、力は大きさ(ここでは矢印の長さ)と向きを持っていることが直感的にわかる。

(2) 2つの力の釣り合い
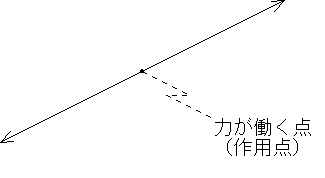
まったく同じ大きさの力が、同じ直線上のまったく正反対にはたらくとき、その二つの力は釣り合う。作用点には力がはたらいていないのと同じである。
(3) 力の合成
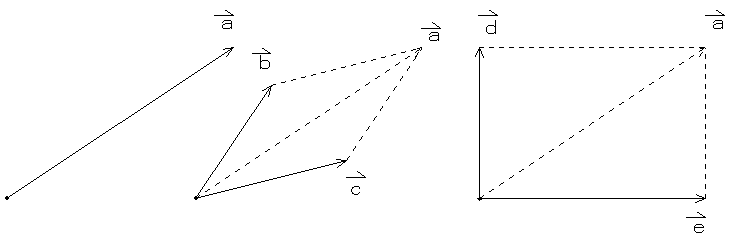
二つの力を合成した力は、その二つの力をそれぞれ平行四辺形の辺としたときの、対角線(の大きさと向き)となる。これが力の平行四辺形の法則である。
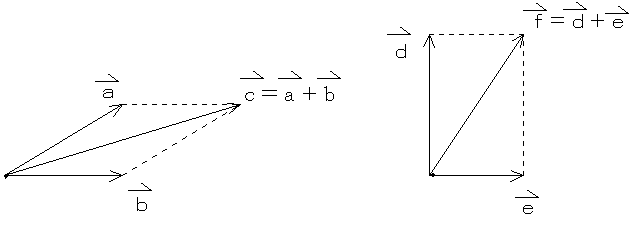
(4) 三つ以上の力の合成
順番に、二つずつを合成していけばよい。
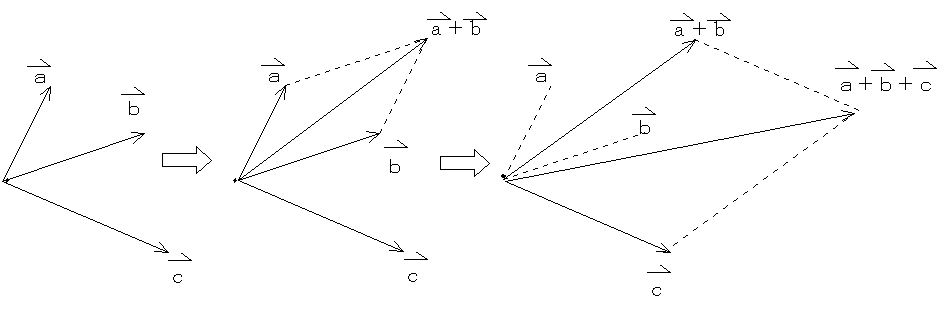
(5) 3つの力の釣り合い
どれか二つの力を合成したもの(図ではa+b)と、向きが正反対で大きさの等しい力(図ではc)が釣り合う。ことのき、b+cがaと、c+aがbと釣り合っていることを確かめてみよう。
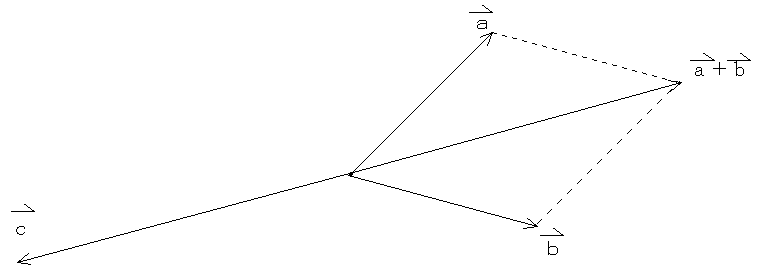
(6) 力の分解
力の合成と逆に、ある力を対角線と考え、、それを対角線とする平行四辺形の2辺に力を分解することができる。真ん中の図ではa=b+c。だから、aはbとcに分解できる。右図のように、aを直角な2成分(dとe)に分解すると便利なことが多い。