第5章 重力(1)
| 目次 | |
| 1. | 重力 |
| 2. | 正規重力 |
| 用語と補足説明 | |
| この章の参考になるサイト | |
1. 重力
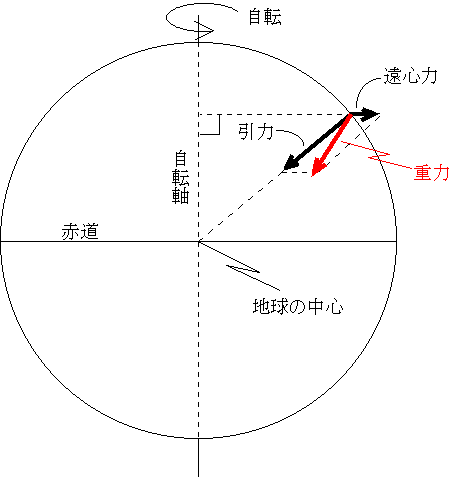
重力は地球の中心に向かう引力と、自転軸から垂直に遠ざかろうとする遠心力の合力である。だから、重力(鉛直線の向き)は両極と赤道以外の地点では地球の中心に向かない。
地球の中心に向かう引力の大きさは、中心からの距離によって決まる。もう少し厳密に言えば、地球の中心からの距離の2乗に反比例する。地球表面上での地球の中心からの距離は、地球の形が球ではなく、回転だ円体である。だから、地球の中心からの距離は赤道で一番大きく、北極・南極で一番小さい。だから、引力は赤道で一番小さく、両極で一番大きい。
一方、地球上では自転の速さ(角速度)は一定なので、遠心力は自転軸からの距離に比例する。だから遠心力は赤道で一番大きく、両極では0(ゼロ)である。
つまり重力は、赤道で一番小さく、両極に向かうほど(緯度が高いほど)大きくなる。両極と赤道での重力大きさの比はこちらを参照。

2. 正規重力
地球上での引力は地球の中心からの距離の2乗に反比例する。その距離は、地球の形(回転だ円体としての形)がわかっていれば、緯度によって決まる。また、自転軸からの距離も、緯度によって決まる。つまり、引力も遠心力も緯度によって決まるので、重力も緯度によって決まることになる。
この緯度によって決まる理論的な重力を正規重力という。
※ 標準重力:緯度45°の海面上での重力。国際度量衡委員会が定めた値=9.80665m/s^2。記号はg(斜体)。ただし、標準重力を正規重力の意味で使っている本もある。たとえば平凡社の地学事典。
引力:引力(万有引力)はニュートンが発見した力である。地球上での引力は、地球の全質量が地球の中心に集まったと考えてよい。こうすると、地球の質量も万有引力の法則から求めることができる。
地球の質量:いま遠心力を考えなくとてもいい北極に質量mの物体をおくと地球の引力により mg という力を受ける。ここで、gは重力加速度である。一方、引力は地球の質量をMとすると、引力は質量の積に比例し、距離の2乗に反比例する力、つまりGMm/r2となる。この二つのはもちろん等しい。
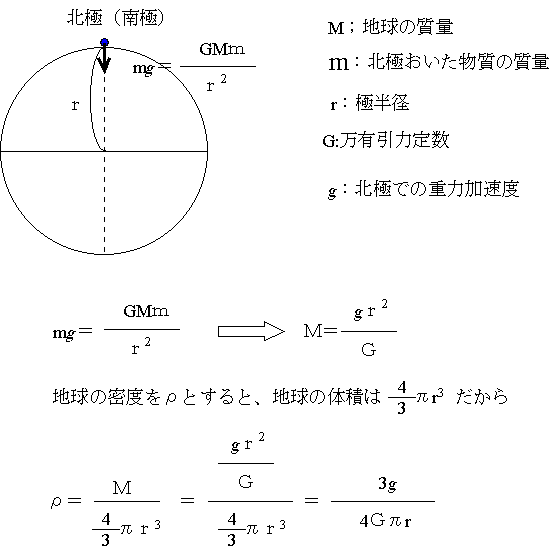
上の式に、重力加速度g=9.8m・s-2、極半径r=6.4×106m、万有引力定数G=6.7×10-11m3・s-2・kg-1を代入して地球の質量Mを求めると、M=6.0×1024kgとなる(正確な地球の質量はM=5.974×1024kg)。
地球の質量は、人工衛星の飛び方(高さと周期)からも求めることができる。
密度は上の式に数値を代入して、ρ=5.5×103kg・m-3(5.5g/cm3、正確な密度はρ=5.52×103kg・m-3(5.52g/cm3))となる。この密度はふつうの岩石の密度(おそそ3.0×103kg・m-3(3.0g/cm3)くらい)よりは大きく、鉄7.7×103kg・m-3(7.7g/cm3)よりは小さい。
なお、上の式から表面重力は下のようになる。
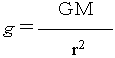
つまり、天体の質量に比例し、半径の2乗に反比例することもわかる。
遠心力:遠心力fは、円運動している物体の質量m、円の半径r、運動の角速度ω(ラジアン・s-1)とすると、f=mrω2となる。地球上では地球の自転の角速度ωは、地球の自転=24時間(60×60×24秒)で2πラジアン(360°)なので、2πrad÷(60×60×24)s=7.3×10-5rad・s-1という一定である。だから、地球の自転による遠心力は自転軸からの距離に比例することになる。
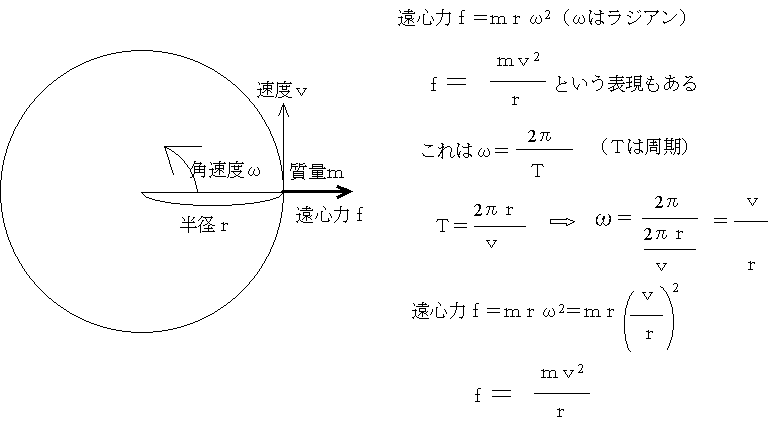
自転軸からの距離が最大にである赤道は遠心力が地球上で一番大きい。また、中心からの距離が一番大きいので引力は一番小さい。そこで赤道半径をRとして、この二つの力を比べてみる。Gは万有引力定数、Mは地球の質量、mは赤道上の物体の質量、ωは地球の自転の角速度(ラジアン/秒)である。
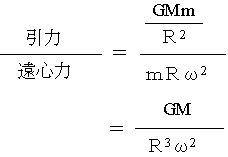
上の数値を使って計算すると、引力の方が遠心力の約290倍の大きさであることがわかる。他の緯度ではこの比の値はもっと大きくなる。
両極と赤道の重力の比:極半径rp=6.356×106m(6356km)、赤道半径re=6378×106m(6378km)を使って、地表に置いた質量mの物体にはたらく極と赤道での重力の大きさの比を計算してみる。地球の質量はM=5.974×1024kg、万有引力定数はG=6.673×10-11m3・s-2・kg-1である。赤道では地球の自転の角速度ω(=7.269×10-5rad・s-1)として、mreω2の遠心力もはたらいている。
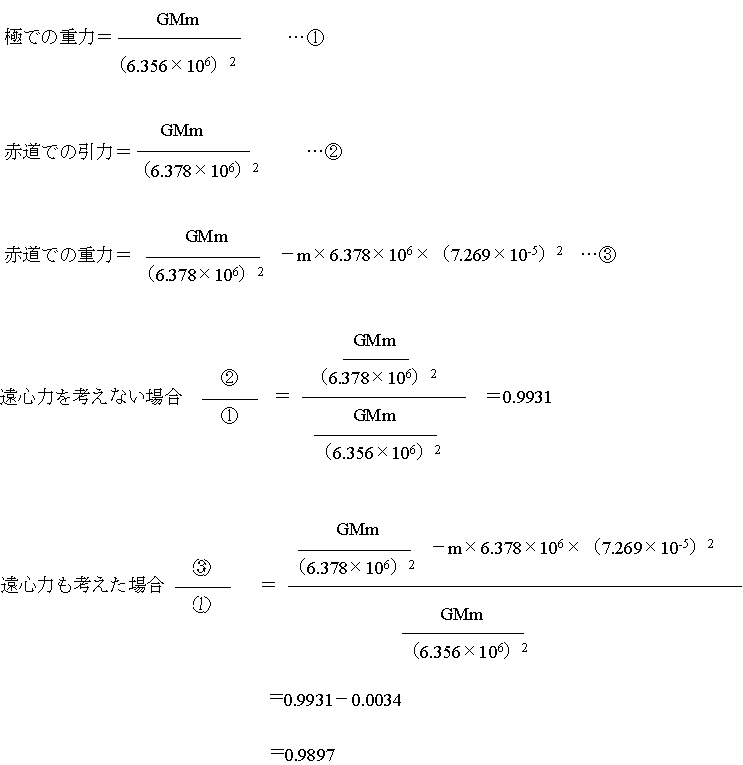
つまり、赤道での重力は極での重力より、1%程度小さくなっていることがわかる。極で体重60.0kgの人は、赤道では59.4kg(600gものダイエット!)になっている。
正規重力の式:正規重力は緯度の関数となっている。緯度φ(ファイ)での標準重力γ(ガンマ)は、赤道上での重力γe、地球だ円体の長軸の長さa、扁平率α(アルファ)として、以下の式で求めることができる。地球だ円体の形(長軸や扁平率)についてはこちらを参照。
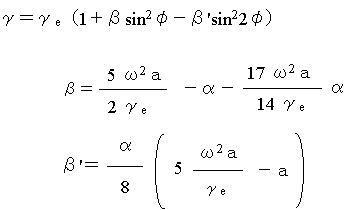
測地学会:http://www.geod.jpn.org/web-text/part2/2-2/index.html