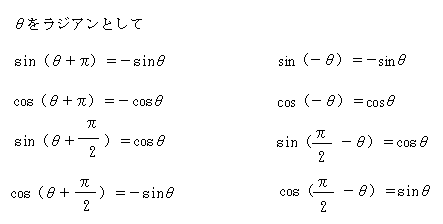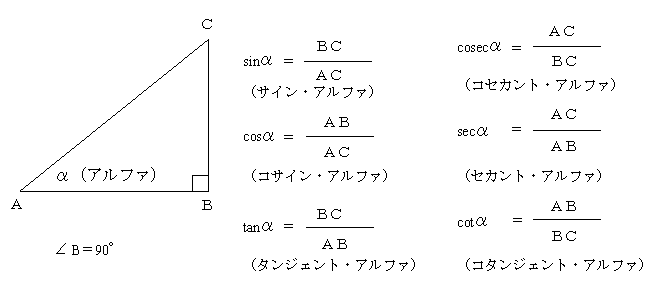
直角三角形において、直角以外のもう一つの角(下の図ではα)の大きさ決めれば、その直角三角形の大きさにかかわらず、各辺の比の値は一定になる。そこで下図のように、sin(サイン、正弦)、cos(コサイン、余弦)、tan(タンジェント、正接)、さらにcosec(コセカント、余割)、sec(セカント、正割)、cot(コタンジェント、余接)を決めることができる。

このとき、下のような関係がある。
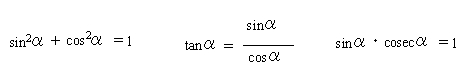
三角比では、∠αは0<α<90°(π/2rd)だが、この角度を一般角にまで拡張したのが三角関数である。理科では波とか振動とかで出てくる。三角関数の場合は角度をラジアンで表わすことが多い。
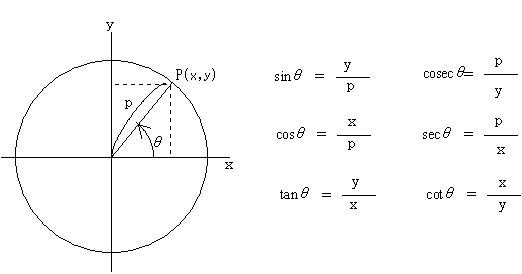
このとき、上のような関係ばかりではなく、下のような関係も成立する。