
月の表面:陸(白っぽい部分)と海(黒っぽい部分):国立天文台一般向け情報(画像・情報)のページ
http://www.nao.ac.jp/Gallery/SolSys/Moon/m010705l.jpg
3. 表面の様子
月の表面には白っぽい部分と黒っぽい部分があり、その黒っぽい部分の形が日本では「ウサギの餅つき」に見えたり、中国では「カニ」やヨーロッパでは「女の人の顔」に見えたりするのである。もちろん同じ模様を見ているのだが、その文化的な背景で見える形が違って見えるのである。
白っぽい部分を陸といい、月の高地である。黒っぽい部分を海といい、月の低地である。もちろん、月には水も大気もないので、海といっても水があるわけではない。
双眼鏡や望遠鏡で月を見ると、火山のカルデラのような窪地がたくさん見える。これはクレータといい、ほとんどが隕石が衝突したときの衝撃でできたものである(ごく一部は火山のカルデラかもしれない)。そのために隕石孔といういい方もある。クレータの直径は200kmを越えるものもある。地球の火山のカルデラの中では最大クラスの阿蘇のカルデラの大きさが23km×14kmであることを考えると、いかに大きいかがわかる。

月の表面:陸(白っぽい部分)と海(黒っぽい部分):国立天文台一般向け情報(画像・情報)のページ
http://www.nao.ac.jp/Gallery/SolSys/Moon/m010705l.jpg

クレータ:国立天文台一般向け情報(画像・情報)のページ
http://www.nao.ac.jp/Gallery/SolSys/Moon/moon1.jpg
月の表面には大気や水がないために、太陽の光を真上から受けている真昼のところでは温度は120℃にもなるが、太陽の光を浴びない夜の部分では-200℃まで下がってしまう。
アポロ宇宙船は月に6回着陸して、月の岩石を合計380kgも持ち帰った。こうして直接調べられた結果によると、月の陸の白っぽい岩石は斜長岩(斜長石という鉱物を多く含む、地球に20億〜30億年前に噴出した火山岩としてアフリカなどに少しある)であり、海の黒っぽい岩石は玄武岩(ハワイや三原山、あるいは中央海嶺で噴出する溶岩など)であることがわかった。また、月の表面は細かい砂(レゴリスという)でおおわれている。
月には大気や水がないので、地球みたいな活発な風化作用・侵食作用はないが、太陽に光を浴びるときと浴びないときの大きな温度差による風化作用、隕石が衝突することに侵食作用があり、他にも宇宙から飛び込んでくる細かい粒子や、太陽からの荷電粒子をもろに浴びている(地球は大気や磁場があり、それである程度防いでいる)。こうして表面は細かい砂にまで砕かれて、レゴリスにおおわれることになる。
月のクレータの中には輪郭がぼけたものがあるが(上の写真参照)、これは大気や水がない月面でも、弱いながらも風化作用・侵食作用が働いていることを示している。つまり、古いクレータほど風化・侵食作用を長い間受けることになるので、輪郭がぼけてしまうのである。逆にいうと輪郭がはっきりとしているものは新しいクレータである。
日本の月探査機「かぐや」が撮影した月の表面の様子(写真)は、宇宙研究開発機構(JAXA)のサイトを参照。
なぜ月の表面には大気や水がないか:結論的には、月の表面重力が小さくて、大気や水(水蒸気)を保持することができないからである。つまり、もし昔大気や水があったとしても、その大気や水を宇宙に逃げてしまうからである。
表面重力(g)は、万有引力定数をG、その天体の質量をM、その天体の半径をrとすると、下の式で求めることができる。つまり、表面重力は天体の質量に比例して、天体の半径に反比例する。
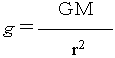
月の質量は地球の質量の0.0123倍、半径は0.272倍(地球の半径6378km、月の半径1738km)であるから、
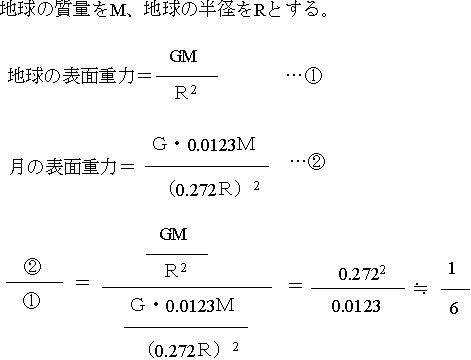
月の表面重力は、地球の約6分の1ということになる。つまり、体重60kgの人は地球上では重さが60kgであるが、月では重さが10kgになってしまう。それだけ、月はものを表面につなぎ止めておく力が小さいことになる。だから、月には大気や水がないのである。もう少し厳密には第2宇宙速度(脱出速度)が小さいので、月には大気や水がないということになる。
第1宇宙速度と第2宇宙速度(脱出速度):高い山からボールを水平に投げるとき、速い速さで投げ出せばそれだけ遠くまで飛んでいく。だから、ある速さ以上の速さで投げ出すと、ボールは地球の中心向かって落ち続けてはいるのだが、地球が丸いために実際には地表に落ちることなく、地球のまわりを回り出す。

この地球に落ちなくなる最低の速さを第1宇宙速度という。第1宇宙速度は人工衛星になる最低の速さである。第1宇宙速度で投げ出したときの軌道は円であり、それ以上の速さで投げ出すと、投げ出したところで一番速く(一番地表に近く)、その反対側で一番遅く(地表から一番遠く)なるような楕円軌道となる。
ケプラーの第3法則から、第1宇宙速度(V1)は天体の質量をM、天体の半径(中心からの距離)をR、万有引力定数をGとすると、下のような式になる。つまり第1宇宙速度は、天体の質量の平方根に比例し、天体の半径(天体の中心からの距離)の平方根に反比例する。
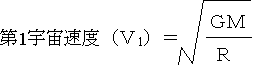
今度はボールを垂直に高く投げ上げてみる。するとボールはだんだんを遅くなり、ある高さで向きを変え、地上には投げ上げたときと同じ速さで衝突する。その向きを変える高さが最高点であり、その点ではボールの速度は0(ゼロ)になっている。また、当然速い速さで投げ上げるほど、高い高さに到達する。ここで、ボールをVという速さで投げ上げたとき、ボールがhという高さにまだ届いたする。このとき、高さhのところでボールをそぉーっと手から離してみると、ボールは地表に向かってだんだん速さを増しながら落ちていき、ある速さで地面と衝突する。この衝突するときの速さは、地表からボールを投げ上げてhという高さに届くときの投げ上げる速さVである。
そこで、宇宙に質量がMである半径Rの天体しかないとして、その天体から無限(∞)の彼方でボールをそぉーっと離してみる。そのボールはその天体の引力で天体に向かって落ち始める。そしてある速さ(V2)で地表に衝突する。無限の彼方から落としても無限の速さで地表に衝突しないのは、万有引力は距離の2乗に反比例する力なので、距離が遠くなるほどどんどん弱い力になってしまうからである。逆にこの速さ(V2)以上の速さで投げ上げれば、その物体はその天体の引力を振り切って、無限の彼方に飛んでいけることになる。そこで、第2宇宙速度を脱出速度ということもある。

この第2宇宙速度(V2)は、天体の質量をM、天体の半径(中心からの距離)をR、万有引力定数をGとすると、下の式で表わすことができる。第1宇宙速度と同じく、第2宇宙速度も天体の質量の平方根に比例し、天体の半径(天体の中心からの距離)の平方根に反比例する。また、第2宇宙速度は第1宇宙速度のルート2倍になっているということもできる。
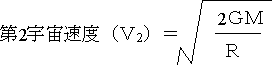
地球の第1宇宙速度は7.9km・s-1、第2宇宙速度(脱出速度)はそのルート2倍の11.2km・s-1である。月の質量と半径は上に書いたように、それぞれ地球の0.123倍、0.272倍であるから、下のように計算して、
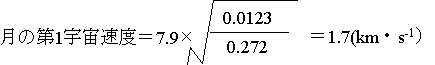
第2宇宙速度はそのルート2倍の2.4km・s-1となる。つまり、月からは地球からの第2宇宙速度(脱出速度)の5分の1ほどの速さで投げ上げると、宇宙の彼方に飛んで行ってしまうことになる。
地球の表面から秒速7.9km以上の速さで打ち上げられたロケットは、地球のまわりを回る人工衛星になり、月の表面から秒速17km以上で打ち上げられたロケットは月のまわりを回る人工衛星になる。また、地球の表面から秒速11.2km以上の速さで打ち上げられたロケットは地球の引力を振り切ることができ、月の表面から秒速2.4km以上の速さで打ち上げられたロケットは月の引力を振り切ることができる。
ただし、地球や月は太陽の引力の束縛のもとにあるので、それぞれの脱出速度を超えても宇宙の彼方に飛んでいくわけでない。宇宙の彼方に飛んでいくためには、地球の表面からは秒速46km(地球の公転の速さは秒速30kmなので、公転方向に打ち出せば秒速16kmとなる)が必要で、これを第3宇宙速度ということもある。第2宇宙速度よりも速く、第3宇宙速度よりも遅い速さで打ち出されたロケットは、太陽のまわりを回る人工惑星となる。
現在の時点(2004年6月)で、第3宇宙速度を超えて打ち出されたロケットは世界でまだ4台しかない。それはすべてアメリカの惑星探査機で、1972年に打ち上げられたパイオニア10号、11号と、1977年に打ち上げられたボイジャー1号、2号の4台である。これらについてはこちらを参照。
なお、これらの探査機は地球から出たときに第3宇宙速度を持っていたのではなく、木星に接近する際にいわゆるスウィングバイ(フライバイ)を行って加速し、その結果も太陽系脱出可能な速度を得たのである。
大気の分子の運動の速さがその天体からの脱出速度を超えてしまうと、分子は宇宙の彼方に飛び去ってしまい、その天体は大気を持てないことになる。月ではその速さが月からの脱出速度を超えてしまった、しかし地球では超えることができなかったということである。
大気の分子の運動:大気を構成している分子はバラバラに飛び回っているが、その平均の速さは温度によって決まっている(大気の温度は大気を構成している分子の平均の速さで決まるといってもよい)。大気を構成している分子の平均の速さは、その大気の絶対温度の平方根に比例し、大気の分子の質量の平方根に反比例する。
300K(27℃)での水素分子(1molが2×10-6kg)の平均の速さは1.9km・s-1(約秒速2km)となる。また、1molが32×10-6kgの酸素分子は、同じく300K(27℃)では水素の1/4の速さの0.5km・s-1ということになる。これはあくまでも平均の速さなので、これ以上の速さで動く分子・原子もある。その速さが天体の脱出速度を超えると、宇宙空間に逃げてしまうということになる。
では、惑星の温度は何によって決まるのだろう。温室効果などをのぞくと、惑星の温度は基本的には太陽からの距離によって決まる。地球と月では太陽からの距離はほぼ同じと考えてよい。だから大気の組成が同じならば、地球と月の温度は同じになってもよい。つまり大気を構成している分子・原子が同じ速さになる。だが、そうすると、表面重力の小さい月では分子・原子の速さが月からの脱出速度を超えてしまうものが次から次に出てくるが、地球ではあまり出てこないので、長い年月の間には月は大気(水蒸気を含む)を失い、地球ではまだ残っているということになる。その地球も、じつは軽い水素をかなり、ヘリウムはほとんどの量を失ったと考えられている。ヘリウムよりも軽い水素の方が残っているのは、水素は水分子(H2O、水素分子の9倍、ヘリウムの4.5倍の質量/mol)の一部になっているからである。
気体分子の運動の速さ:気体の分子運動の速さは、下の式で求めることができる。

つまり、300K(27℃)のときの水素分子の平均の速さは1.9km・s-1(約秒速2km)となる。酸素分子1molは水素分子1molの16倍の質量があるので、同じ温度のときの速さは質量の平方根(この場合は4)に反比例するので、水素分子の4分の1の約秒速0.5kmとなる。
第2宇宙速度(脱出速度):いま宇宙には質量M、半径Rの天体と、質量m(大きさは無視できる)があったとする。この二つの間には距離(r)の2乗に反比例する力(万有引力)が働く。だから、無限の彼方から天体の表面までその二つの間にはたらく力を積分すると位置のエネルギーが出る。無限の彼方からものを離ししたとき、そのものが天体の表面に小とするときの速さはその位置のエネルギーに等しい。このように考えて計算すると、下のような第2宇宙速度の式を求めることができる。

スウィングバイ(スイングバイ):探査機がわざと天体をかすめて飛ぶことによって加速すること(加速する技術)。
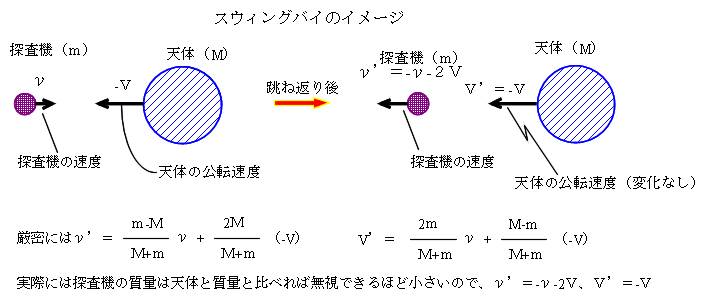
もし、質量mの探査機が、質量Mの天体にぶつかって跳ね返されたとすると(完全弾性衝突したとすると)、天体Mに太陽から見てνという速さ(天体Mから見るとν+Vという速さ)で近づいてきた探査機は、跳ね返ったあとも天体Mから見ると、νという速さ(向きは正反対)で天体Mから遠ざかるように見える。つまり、この探査機は太陽から見るとν+2Vという速さ(向きは衝突前と逆向き)になっている。こうして、探査機mは天体Mの公転の速さをもらって(厳密には運動量と運動エネルギーをもらって)加速したことになる。
本当はこのように正面から近づいては衝突してしまうので、斜めから接近して、逆の方向に抜けていく。下図左のように、探査機が天体に衝突するように近づけば加速スウィングバイ、追いかけるように近づけば減速スウィングバイとなる。
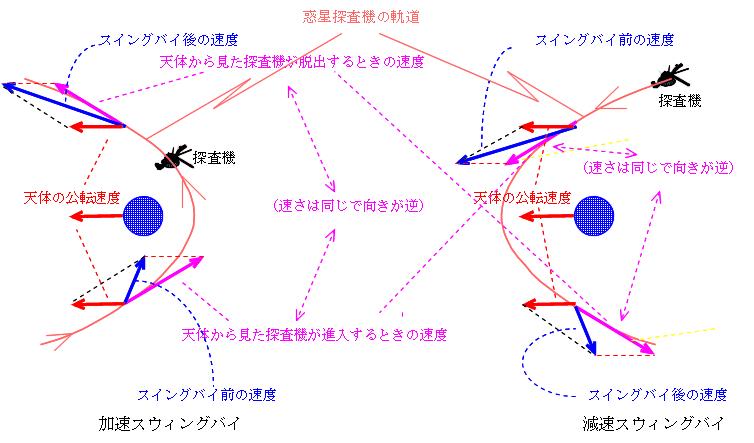
実際には大変な技術で、、小惑星イトカワを目指した「はやぶさ」が地球を利用して行った例では(2004年4月)、地球からの位置の誤差1km以内、速さの誤差1cm/s以内が要求され、それを達成したという。
月探査情報ステーション:http://moon.jaxa.jp/ja/index_fl.shtml