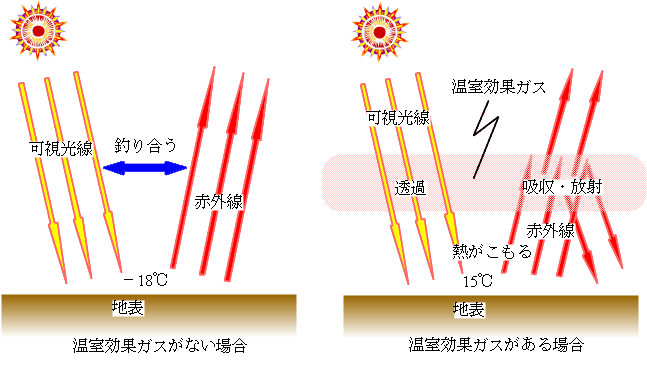
図6-3 温室効果
複雑な地球環境を研究するには、どのような手法が必要であろうか。
(1) 地球の温度と温室効果
地球の温度は、大きく見れば太陽からの放射エネルギー(地球が受け取るエネルギー)と、地球からの放射エネルギーが釣り合うところで決まる。物体が放射するエネルギーは、物体の表面積が一定ならば、その物体の表面温度(絶対温度)の4乗に比例している。これをステファン・ボルツマンの法則という。式で書くと
E(J)=σT4 ここで、
地球の位置での太陽放射(太陽定数)は1.37×103J/秒・m2、それを地球全体に平均するとその1/4(1・2の(1)参照)、また地球の反射能(アルベド)は0.3だから(吸収しているのは0.7だから)、地球(地表と大気)が吸収している太陽放射は結局1.37×103J/秒・m2×0.7=2.40×102J/秒・mである。地球もこれと同じだけのエネルギーを放射しなくてはならない。この値をステファン・ボルツマンの法則に代入すると、
2.4×102(J・s-1・m-2)=σT4 σ=5.67×10-8(J・s-1・m-2・K-4)
T4=4.23×109(K)
T=255(K) (0℃=273Kだから255K=−18℃)
地球の温度は255K(−18℃)となる。これは実際の地表の温度より約33℃も低い。
なお、この詳しい計算についてはこちらも参照。また、<1・2 食料>で用いた太陽エネルギーは、地表が吸収しているエネルギー(地表に到達するエネルギー)で、上で用いている太陽エネルギーは地表+大気(対流圏の大気)が吸収しているエネルギーであることに注意。
地球の温度が単純な計算値より高いのは、地球の大気には水蒸気や二酸化炭素、さらにはメタン、窒素酸化物、オゾン、フロンガスなどの温室効果ガスが含まれているためである。温室効果ガスは、太陽からの放射エネルギー(おもに可視光線)は通すが、地球から宇宙に出ていこうとする放射エネルギー(赤外線)を抑えるのである。そのために熱がこもって、ステファン・ボルツマンの法則から期待される温度よりも高い温度になってしまう。
※ 物体が放射する電磁波の最大強度の波長はその物体の表面温度で決まる(ウィーンの変位則)。太陽のように表面温度が6000℃(5800K)の物体の最大強度は460nm(ナノメートル、黄色に見える)で、そのまわりの波長の電磁波が可視光線。そこで、太陽の放射エネルギーは大部分は、可視光線として放射されている。一方、地球程度の温度(-18℃であろうが、15℃であろうが)では、放射エネルギーは赤外線となる。

図6-3 温室効果
これをもう少し詳しく見てみよう。大気がない場合の地球(つまり月(※1))の放射エネルギーはステファン・ボルツマンの法則に従い、表面温度の4乗に比例する。このとき、太陽放射と釣り合う温度(図6-4のA点=約マイナス18℃)が月全体の平均温度であり、地球に大気がなかった場合の地球の温度ともなる。
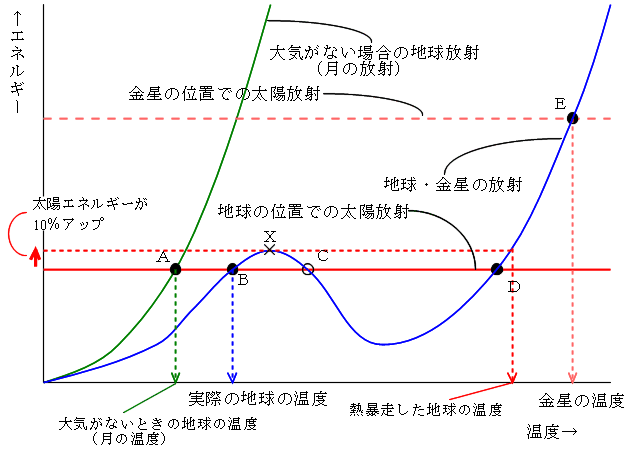
図6-4 地球の温度と地球からの放射エネルギーの概念図:自然の数理(筑摩書房、数理科学シリーズ、1975年)などから作成
もし、太陽の放射がいまより少し(10%くらい)大きくなったり、あるいは人間が作り出すエネルギーが大きくなりすぎてX点を超えてしまうと、地球は熱暴走を始め、海水はすっかり蒸発、石灰岩もすべて分解して、やっとD点(細かくいうとD点より少し温度の高いところ)で釣り合うようになる。そのとき地球の大気圧は水蒸気270気圧、二酸化炭素30〜50気圧の合計300〜320気圧、温度も200℃を越えるだろう。実際に、金星がこの状態である(図のE点)。金星は地球の90倍(90気圧)の大気を持ち、またその95%以上が温室効果ガスである二酸化炭素であるために、その温度は460℃〜480℃にもなっている(※2)。
いくら人間が無限の、しかもクリーンなエネルギー源を開発しても、それを地球で使えば最終的には熱になる。熱暴走を起こさないためには、太陽エネルギーの10%以下に抑えなくてはならないこともわかる。実際には、こんなに使う前に地球の環境は完全に破壊されるであろう。
※1 月のアルベド(反射能)は0.07なので、これを使って計算すると月の温度は276K(3℃)になる。
※2 金星のアルベドは0.78もあり、地球よりも太陽に近いのにもかかわらず吸収している太陽エネルギーは地球よりも小さい。
補足:安定な平衡と不安定な平衡
図6-4で、地球放射と太陽放射が釣り合う点が3つある。B点とD点は、地球の温度が上がれば太陽放射より地球放射の方が大きくなり、出ていくエネルギーの方が大きくなるので温度が下がる。逆に、地球の温度が下がれば太陽放射より地球放射の方が小さくなり温度は上がる。ここは、負のフィードバックがかかっている。つまり、この点は地球の温度がちょっと変動しても必ず元に戻る。このような平衡を安定な平衡(釣り合い)という。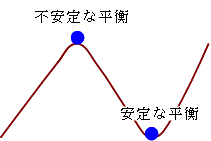
安定な平衡、不安定な平衡は、坂に球(ボール)を止めることを考えるとわかる。右図の青い球は谷底と頂上で止まる。その青い球は、谷底では位置が少しずれても谷底に戻るが、頂上では少しでも左右にずれると坂を転がり落ちてしまう。谷底が安定な平衡のイメージ、頂上が不安定な平衡のイメージである。