
セシウム原子時計(日本標準時グループ)
http://jjy.nict.go.jp/mission/page2.html
7. 時刻
もともと時刻と、時刻と時刻の間の長さ(時間)は地球の運動をもとにして決められた。
a. 恒星時
春分点の時角を恒星時という。 時角とは真南から西回りに0時〜24時で測る角度である。だから、春分点が南中したら恒星時は0時、真西に来たら6時、地球の反対側に来たら(見えないが)12時、真東に来たら18時となる。
実際には春分点(の近く)には、天の北極近くにあるような北極星はないし、いつも春分点が見える位置にあるわけでもない。そこで、赤経(α)がわかっている恒星の時角(t)を観測することによって、春分点の時角がわかる。図はこちらを参照。
恒星時=春分点の時角 ←→ 恒星時=ある恒星の赤経(α)+その恒星の時角(t)
b. 太陽時
恒星時は、ある時刻が夜明けになったり、真昼になったり、夕方になったり、真夜中になったりと、日常生活では不便である。そこで、われわれは太陽の時角をもとにした時刻を使う。ただし、太陽が南中したときを正午(12時)としたいので、時角に12時を足して
太陽時=太陽の時角+12時
とする。こうすればいつでも、日が昇るころは6時ころ、太陽が南に来れば12時、西に沈むころは18時となって都合がよい。
c. 平均太陽時
実際の太陽をもとにして決めた時刻を真太陽時という。真太陽時は日時計が示す時刻である。だが、真太陽時は、見かけ上の太陽の天球上の動きが一定でないことから、それを使うと1日の長さが日ごとで異なることになる。そこで、実際には見えない平均太陽をもとにした時刻を定義する。
平均太陽時=平均太陽の時角+12時
真太陽時と平均太陽時の差を均時差という。
均時差の値は理科年表(丸善)のようなデータ集に出ている。これを使えば、実際の太陽の時角から、平均太陽時を求めることができる。日時計を使って時刻(平均太陽時)を求めるときは、均時差のデータ表が必要である。
この平均太陽の南中から南中までの時間を1日=24時間とする。24時間の24分の1が1時間、1時間の60分の1が1分、1分の60分の1が1秒という具合に時間の長さも同時に決まる。
d. 標準時
太陽が南中する時刻は東ほど早く、西ほど遅い。つまり経度によって異なる。だから地球上では無限の時刻が存在してしまうことになる。それでは不便なので、ある地域を代表する時刻を決める。日本では東経135°での平均太陽時を日本標準時(JST)としている。世界標準時は経度0での平均太陽時である。
地球の自転は24時間で360°だから、1時間で15°回転する。つまり、経度が15°違うごとに時刻は1時間ずつずれる。また、東ほど早い。日本標準時は東に135°だから、世界標準時よりも9時間早い時刻である(進んでいる)。日本では、世界標準時が0時のとき9時、6時のとき15時、12時のとき21時である。そして、18時のときは27時となるが、これは次の日の3時のことである。
一般にその地域の標準時は、経度15°刻み(1時間単位のずれ)になっていることが多い。ただし、国によっては世界標準からは30分単位のずれで、その地域の標準時を設定しているところもある。また、季節によってわざと時計を1時間進める「サマータイム」を設けている国もあるので注意が必要である。
東へ行くとどんどん時刻が早くなっていき、地球を一周してしまうと24時間早い次の日の同時刻になってしまう。逆に西回りで一周すると前の日の同時刻になってしまう。こうしたことを避けるために、東経180°(西経180°)に沿って(実際は国境などを考慮して)、日付変更線が設けられている。日付変更線を西から東にまたぐときは日にちを1日戻し、逆に東から西にまたぐときは1日進める。
例えば日本からアメリカ本土に渡るときは日にちを1日戻し、アメリカから日本に戻るときは1日進めることになる。
正確な時計があり、それにより正確な標準時がわかれば、天体(太陽)観測でその場所の経度を求めることができる。緯度も太陽のデータから求めることができる。実際の例は下を参照。
e. 原子時
原子の振動は地球の運動よりも正確であることがわかった。つまり、地球の自転は結構ふらついているのだ。平均的には、地球の自転は遅くなっている。だから一時は、自転よりも安定している地球の公転をもとにして1秒という時間を決めた時代もある。現在では1秒の長さは原子の振動をもとにして決められている。
1秒=セシウム133が9192631770回振動する時間。
この原子の振動を利用して時を刻む時計が原子時計である。

セシウム原子時計(日本標準時グループ)
http://jjy.nict.go.jp/mission/page2.html
f. 協定世界時
いくら自転周期が一定でないとはいえ、それはごくわずかのずれだし、日常生活ではやはり1日の長さは太陽を基準にした方が便利である。そこで、1日の長さは平均太陽時を生かし(太陽日を使い)、1秒の長さは原子時を使うことにする。この原子時の1秒をもとにした1日の長さが、平均太陽日よりも0.9秒以上ずれたら、補正することとする。この補正を“うるう秒(閏秒)”という。地球の自転は平均的には遅くなっているので、うるう秒を加えることが多い。過去のうるう秒のデータは、日本標準時グループのうるう秒のページを参照。
補正は世界標準時の12月31日と1月1日の間で行う(日本標準時では1月1日の午前9時になる)。12月31日59秒のあとに12月31日60秒を入れるのである。その1秒後が1月1日0秒となる。これで足りなければ6月30日と7月1日の間、これでも足りなければ3月31日と4月1日の間という具合に行う。
原子時で補正された平均太陽時を協定世界時(UTC)という。この協定世界時が世界で使われているものである。だから厳密には、日本標準時は協定世界時+9時ということになる。日本標準時は、情報通信研究機構の日本標準時グループ(トップページ)が管理している。
8. 暦
暦のもととなる1年は1太陽年で、その長さは365.2422日である。そこで平年の365日に対し、1年が366日であるうるう年(閏年)を入れて補正する。現在の補正の仕方はグレゴリオ暦と呼ばれるものであり、
西暦が4で割り切れる年はうるう年。
ただし、西暦が100で割り切れる年は平年。
でも、西暦が400で割り切れる年はうるう年。
という決め方である。例えば西暦1900年や2100年は4で割り切れるが、100でも割り切れるので平年。しかし、西暦2000年は100で割り切れるが、さらに400でも割り切れるのでうるう年に戻る。
グレゴリオ暦は結局、400年間で97回のうるう年を入れて補正していることになる。(365日×303+366日×97)÷400年=365.2425日/年。つまり1年を365.2425日としている暦である。これは1太陽年とは0.0003日のずれである。だから、約3333年たつと1日のずれとなる。1500年後あたりに調整しないとダメということである。
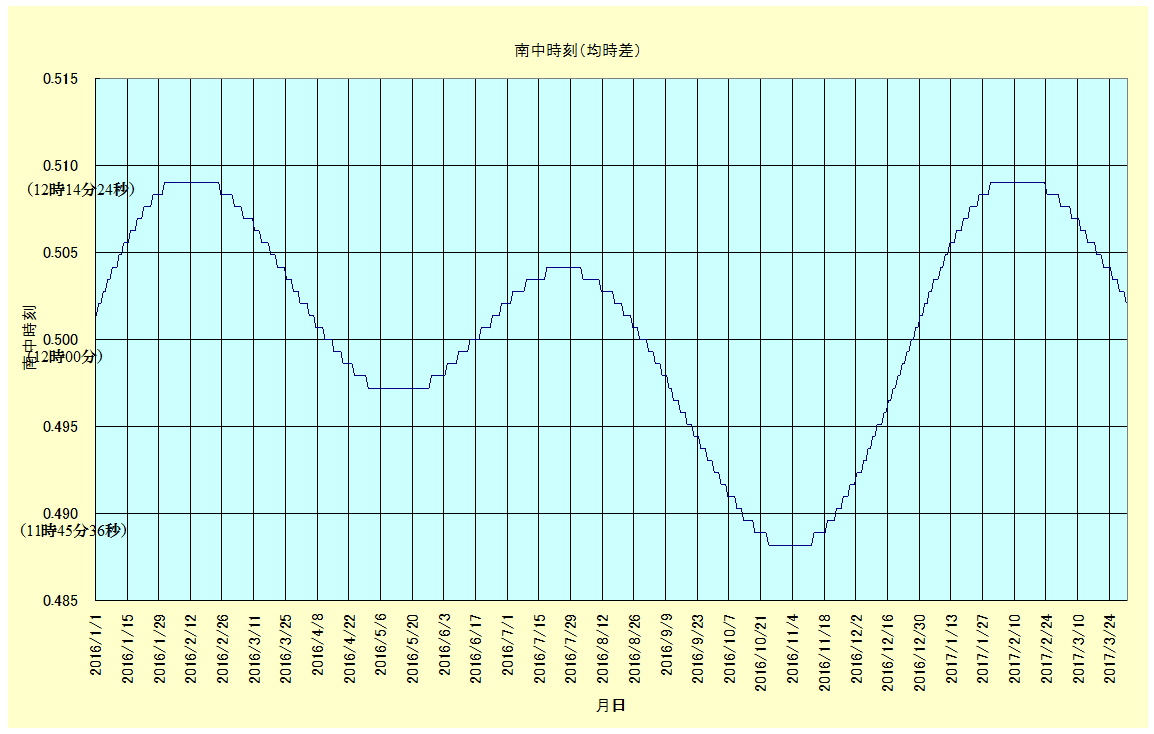
均時差:下のグラフは、国立天文台のデータを使った描いた均時差のグラフである。用いたのは日本標準時子午線(東経135°)に近い神戸のものである。実際の太陽(真太陽)を使った時刻(例えば太陽が南中したとき=12時)と、平均太陽の時刻(例えば標準時の経度(日本では東経135°)の差を考慮した時刻、東京(東経140°では標準時よりも20分進んでいる)の差(均時差)は、最大でプラスマイナス15分くらいのずれがあることになる。日時計が示す時刻は真太陽が示す時刻(視太陽時)なので、日時計が示す時刻から標準時を求めるためには、その土地における標準時との時差、さらにその日の均時差のデータがわからないとならない。
※ 国立天文台のデータ:http://eco.mtk.nao.ac.jp/koyomi/dni/dni29.html
※ 図の作成に使用したExcelファイル:../../rika-kyoiku/kobenohinodehinoiri.xls
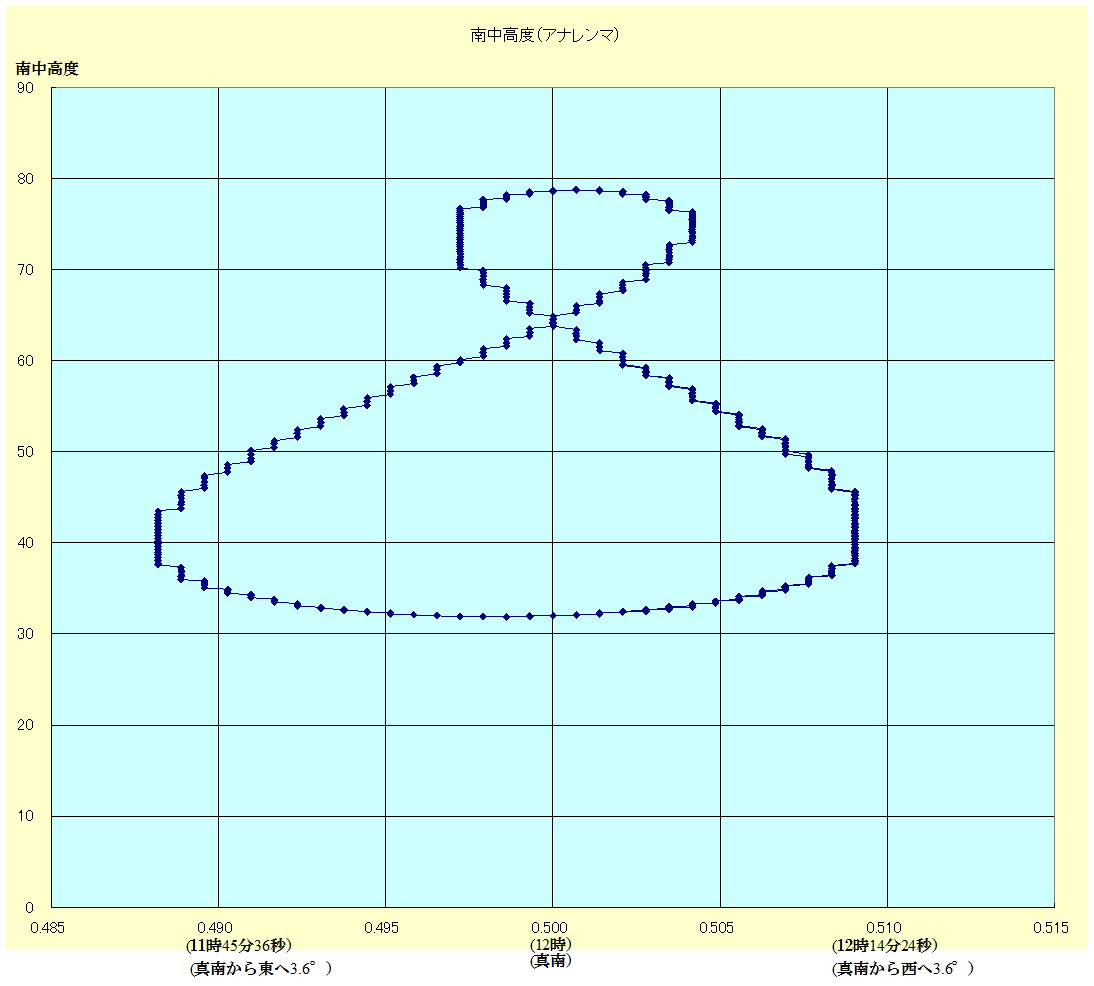
アナレンマ:均時差があるために、実際の太陽は特別な日をのぞくと12時には南中しないことになる。また、太陽は季節によって南中高度が異なる。こうして、12時(平均太陽時)の時の実際の太陽の位置の太陽の軌跡をアナレンマという。アナレンマは“8の字”の形となる。上の国立天文台のデータを使って神戸でアナレンマを描くと下のようになる。
 |
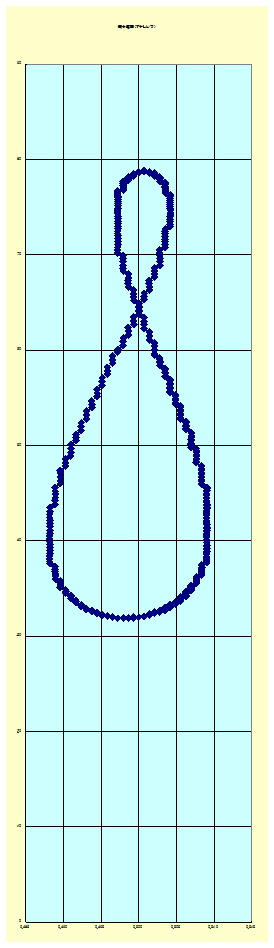 |
| 実際にはこのような細長い“8の字”になる。 | |
 |
|
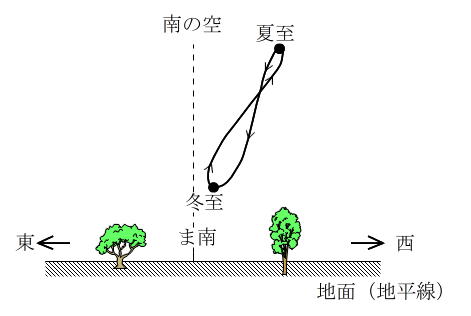
| 東京におけるアナレンマの模式図。東京(東経140°)の地方時は日本標準時(東経135°)よりも20分進んでいるので、アナレンマが真南よりも西にずれる。 | |
 |
 |
| アナレンマを利用した日時計(ヨハネスブルグ近郊スタークフォンテン洞窟(アウストラルピテクス遺跡)) | アナレンマ上のその日の太陽の位置に棒を垂直に立てたとき、その影がそのときの時刻を示す。均似差を盛り込んでいるので、均似差の補正なしに正確な時刻が求まる。 |
緯度と経度の決定:正確な時計と均時差のデータがあれば、太陽(赤道座標がわかっているとして)を観測することで、自分の位置(緯度と経度)を決めることができる。例えば理科年表2004を見ると、2004年5月5日の太陽の赤道座標は、2h49m30s(2時49分30秒)であり、赤緯+16°17.2′、また均時差は+3分18.8秒である。
この2004年の5月5日に、ある場所で日本標準時の12時20分41.2秒に太陽が南中し、その南中高度は62°57.2′であったとする。この場所の経度と緯度を求めてみる。
この場所で太陽が南中しているので、ここでの真太陽時は12時。この場所での平均太陽時は、平均太陽時=真太陽時-均時差だから、12時-(+3分18.8秒)=11時56分41.2秒となる。これは日本標準時(東経135°での平均太陽時)よりもちょうど24分早い。1°東に行くごとに4分ずつ早くなるので、6°東の東経141°であることがわかる。このとき標準時を示す時計が正確でないと、経度が正確に求まらないことがわかる。
また南中高度は、緯度φ(ファイ)の地点の赤道座標の真南での高度は(90°-φ)、赤緯δ(デルタ)の天体の南中高度h=(90°-φ)+δである(下図参照)。いまh=62°56.4′、δ=+16°17.2′を代入して、62°57.2′=(90°-φ)+16°17.2′。これより、φ=43°20′を得る。
東経141度、北緯43°20′を地図で見てみると、北海道の小樽市付近ということになる。このように、その場所の経度・緯度を求めることができた。
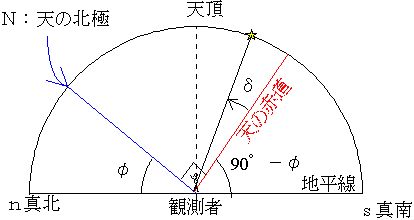
もちろん、上の図からもわかるように、緯度求めるには天の北極の高度(ほぼ北極星の高度)を観測してもよい。
正確な機械時計(クロノメーター):振り子の等時性の原理はガリレオ(イタリア、1564年〜1642年)によって発見された。それを利用した振り子時計は、17世紀の後半、ホイヘンス(オランダ、1629年〜1695年)やフック(イギリス、1635年〜1703年)によってつくられた。しかしどう工夫しても、遠洋航海に出ると時計が狂ってしまうことがわかった。
つまり振り子の周期は、振り子の長さの平方根に比例し、重力加速度の平方根に反比例する。振り子のゆれる周期(T(秒))は、振り子の長さl(m)、重力加速度g(m・s-2)、円周率をπとすると下の式のようになっている。
![]()
ある場所から動かなければ、重力加速度は一定と見なしてよいので、振り子の長さを変えなければ周期は一定である。これが振り子の等時性である。しかし、温度の変化により振り子の長さが異なれば、振り子の周期もことなり、振り子を利用した時計は狂うことになる。もう一つ、重力も地球上ではごくわずかだだその値を変える。赤道に近づくほどその値が小さくなるので、振り子の周期は長くなり、振り子を利用した時計はこのためにも狂うようになる。
このために、18世紀の初めにイギリスは賞金を出して、時計の高精度化に挑ませた。賞金を獲得したのは、イギリスの時計師ハリソンで、彼は1728年から1759年までに4種類のクロノメーターを完成させた。最後のものは、当初のイギリス政府の目標である2か月の航海で2分以内の誤差をはるかに上回る、81日間で誤差5秒以内という時計だったという。
その後水晶発振の原理を利用した水晶時計がつくられると、こうした機械式のクロノメーターは使われなくなった。現在ではGPSや電波時計によって、正確な時刻がわかるようになっている。
自転の遅れ:自転は微妙で、地球全体の気圧配置や、降雪の重さなどによってもふらつくことがある。だが、地球の自転対して一番影響が大きいのは、潮汐である。潮汐による海水と海底の摩擦が地球の自転に対してブレーキをかけるのである。だから、平均すると地球の自転はだんだん遅くなっている。
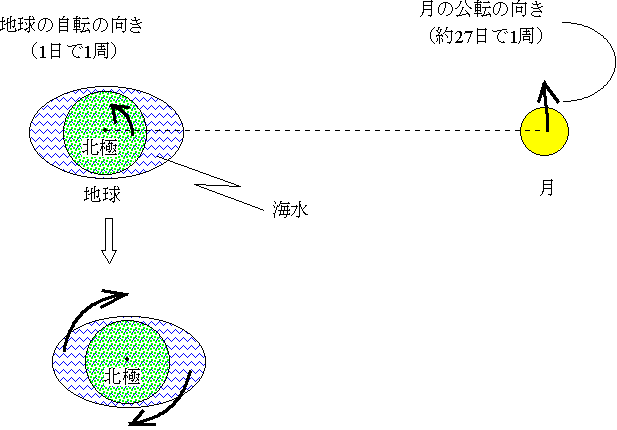
潮汐(潮の満ち引き)は、おもに月の引力(厳密には月の引力が地球の場所ごとによってその大きさが異なる、その差=潮汐力)によって生ずる。結果としては、月に面した側と反対側の海面が盛り上がる。これを地球の北極の上から見たのが下の図である。この海水が膨らんだところに注目すると、これはほぼ月の方向である。下図のように地球は1日で1回転するのに、月が地球のまわりを回るには27日かかる。だから月に引かれて海水の膨らんだ部分の動きは、地球(堅い部分)の自転の動きよりもはるかに遅いことになる。
だから、地球上でこの海水が膨らんだ部分の動き(満潮になっている場所)を見ると、それは東から西に動いているように見える。この向きは地球の自転の向きと逆である。つまり、この潮汐による海水の動きは、地球の自転にブレーキをかけるようにはたらく。このために、地球の自転は長い目で見るとだんだん遅くなるのである。
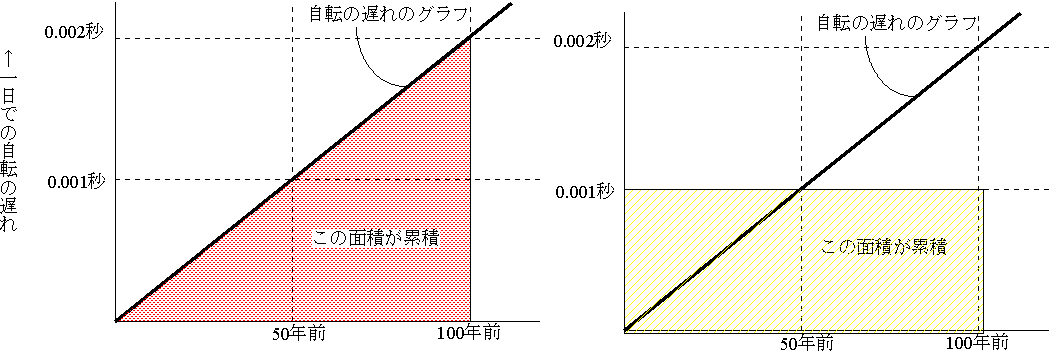
この潮汐による地球の自転の遅れは、この100年で0.0017秒というわずかなものである。つまり、100年前の1日は、いまの1日よりも0.0017秒短かったということになる。だが、このわずかのずれも累積していく。100年間で約0..002秒のずれとして、その累積を計算してみる。
下の右図の赤い色を付けた部分の面積が、毎日毎日のずれが100年間(365×100日間)での累積となる。下右図からわかるよう、この面積(赤い部分)は、毎日がずれの平均値0.001秒ずつ遅くなったとして、その累積を求めた量(下右図の黄色い部分)と同じである。結局累積は、
0.001秒・日-1×365000日=36.5秒となる。
1000年間では同じように考えて、1000年後の1日は今と比べて0.02秒長くなるので、その平均は0.01秒/日、累積は
0.01秒・日-1×3650000日=3650秒(約1時間)
このごくわずかの地球の自転の遅れも、このように累積していくと思わぬ長さになる。
では、地球の自転はどこまで遅くなるのだろう。月が地球に対して同じ面を向けているように、地球もいつかは月に対して同じ面を向けることになる。そうすると、もう潮汐によるブレーキはかからなくなる。そのときの1日の長さは約60日(もちろん今の時間で)となるらしい。そして、そうなったときの月は現在よりはるかに遠いところに行くはずである。実際、アポロが月面に設置した反射鏡を使って、レーザ光線で月までの距離を正確に測ると、月は毎年3.8cmずつ遠くなっていることが確認されている。
時間を逆転して、過去に遡るとどうだろう。2億年前前の1日は23時間、3億年前の1日は22.8時間、4億年前では22.2時間、5億年前では21.2時間となる。地球の公転周期はあまり変わっていないらしいので、1年の日数は、2億年前は380日、3億年前は384日、4億年前は395日、5億年前は415日ということになる。
なお、この項の数値は、「太古、月は近かった(生きている地球の新しい見方)」(大江昌嗣、グバプロ、1999年)を参考にしている。
うるう秒の挿入:2006年1月1日に、7年ぶりにうるう秒が挿入された。これは日本時間では午前8時59分59秒と午前9時0分0秒の間になる。具体的にはふつうは午前8時59分58秒、59秒、午前9時0分0秒となるが、この日は午前8時59分58秒、59秒、60秒、午前9時0分0秒となった。詳しくは日本標準時グループのページを参照。
 |
 |
| 情報通信研究機構(小金井本部)のデジタル時計が8時59分60秒(一番上が日本標準時)を示している。2段目は世界標準時。一番下は、協定世界時−国際原子時。上の写真は“60秒”の表示を取材する報道陣。 http://www.nict.go.jp/publication/NICT-News/0602/p05.html |
2012年7月1日、「うるう秒」挿入の瞬間(情報通信研究機構(小金井本部)のデジタル時計。 http://jjy.nict.go.jp/QandA/data/leapsec-rep2012.html |
 |
|
| 2017年1月1日のうるう秒(http://www.nict.go.jp/JST/JST5.html) | |
 |
左の画像をクリックすると、2017年1月1日のうるう秒の様子を動画でご覧いただけます。 |
ただしNTTの117番で得られる時報では、「お客さまが時報サービス「117」番を聞かれた時に自然な形となるように、平成18年1月1日(日)、午前8時58分20秒から午前9時00分00秒までの100秒間に時報サービス「117」番の秒音を100分の1秒ずつ長くして、時刻を1秒遅らせ、午前9時ちょうどに日本標準時に合うようにします。」という調整を行った。NTTのサイトを参照。
※ 2015年7月1日のうるう秒のときNTT東日本は、「8時59分60秒」を1秒挿入し、日本標準時刻に合うようにします。」という対応を行った。
https://www.ntt-east.co.jp/release/detail/20150610_01.html
また国際電気通信連合はうるう秒の廃止を検討している。うるう秒の挿入はカーナビ、通信システム、株取引などに影響を与えるということらしい。原子時だけを使って時刻(時間)を決定すべきということになる。これに対して天文学者は、時間(時刻)と地球の自転を切り離すべきではないし、実際にも、観測衛星との通信には地球の向きを知らないとできないという問題も生ずるとして、うるう秒の廃止に反対している。うるう秒廃止については、日経サイエンス2006年01月号参照。下サイトも参照。
http://jjy.nict.go.jp/%E3%81%86%E3%82%8B%E3%81%86%E7%A7%92%E8%AA%AC%E6%98%8E%E4%BC%9A%E7%94%A8%E8%B3%87%E6%96%992015.pdf
http://globe.asahi.com/feature/100111/side2/01_03.html
下は現行の「協定世界時」になって以降(1972年以降)、2017年までのうるう秒の一覧表である。不定期に27回うるう秒が挿入されていることがわかる。
第 回 年 月 日 うるう秒 協定世界時-国際原子時
27 2017年1月1日
+1 秒 -37秒
26 2015 年 7月 1日 +1 秒 -36秒
25 2012 年 7月 1日 + 1 秒 -35 秒
24 2009 年 1月 1日 + 1 秒 -34 秒
23 2006 年 1月 1日 + 1 秒 -33 秒
22 1999 年 1月 1日 + 1 秒 -32 秒
21 1997 年 7月 1日 + 1 秒 -31 秒
20 1996 年 1月 1日 + 1 秒 -30 秒
19 1994 年 7月 1日 + 1 秒 -29 秒
18 1993 年 7月 1日 + 1 秒 -28 秒
17 1992 年 7月 1日 + 1 秒 -27 秒
16 1991 年 1月 1日 + 1 秒 -26 秒
15 1990 年 1月 1日 + 1 秒 -25 秒
14 1988 年 1月 1日 + 1 秒 -24 秒
13 1985 年 7月 1日 + 1 秒 -23 秒
12 1983 年 7月 1日 + 1 秒 -22 秒
11 1982 年 7月 1日 + 1 秒 -21 秒
10 1981 年 7月 1日 + 1 秒 -20 秒
9 1980 年 1月 1日 + 1 秒 -19 秒
8 1979 年 1月 1日 + 1 秒 -18 秒
7 1978 年 1月 1日 + 1 秒 -17 秒
6 1977 年 1月 1日 + 1 秒 -16 秒
5 1976 年 1月 1日 + 1 秒 -15 秒
4 1975 年 1月 1日 + 1 秒 -14 秒
3 1974 年 1月 1日 + 1 秒 -13 秒
2 1973 年 1月 1日 + 1 秒 -12 秒
1 1972 年 7月 1日 + 1 秒 -11 秒
1972 年 1月 1日 ― -10 秒
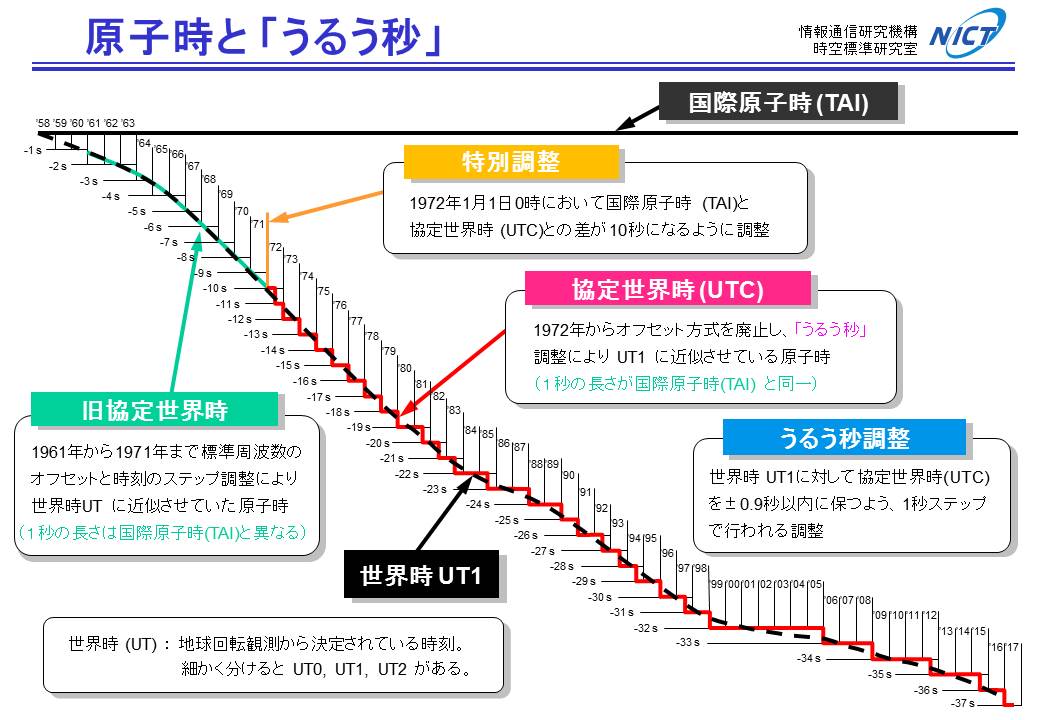
協定世界時などとうるう秒の関係(日本標準時のページ:http://jjy.nict.go.jp/QandA/reference/leapsec-addendum2017.html)
電波時計:日本標準時グループは日本の標準時を管理している。そして、その日本標準時を電波に乗せて標準電波(JJY)として発信している。テレビなどの時報がこれをもとにしている。電波の発信アンテナは、「おおたかどや山標準電波送信所」(福島県・田村郡都路村/双葉郡川内村)とはがね山標準電波送信所」(佐賀県佐賀郡富士町/福岡県前原市)の2箇所にある。
最近では、この電波を受信して時刻を合わせる機能を持つ電波時計が普及しだした。標準電波が受信できさえすれば、テレビなどの時報とまったく同じ時刻、つまり日本標準時を正確に表示できる。この電波時計は、時刻合せの必要がない正確無比(日常生活上では誤差がないとしてよい)の時計である。
 |
 |
| 壁掛け型の電波時計 | 腕時計。向かって左の合成樹脂の中に標準電波の受信用アンテナがある。最近の機種では、こうしたアンテナは目だなくなっている。 |
グレゴリオ暦:昔、暦は月の満ち欠けを利用して1か月を30日、1年を12か月として、季節の巡りとのずれが大きくなったらうるう月(閏月)を入れて調整する太陽太陰暦を使うところが多かった。ところが、エジプトでは1年を周期とするナイルの氾濫が起きるので、昔から原始的な太陽暦が使われていた。
ローマのシーザー(ユリウス・カエサル、紀元前100年〜紀元前44年)は、エジプトに遠征したときにこの太陽暦を学び、それまでのローマで使われていた太陽太陰暦(1月30日×12か月+月に属さない約60日)を廃止して、紀元前46年にユリウス暦を制定した。ユリウス暦は、4年に1回うるう年を入れる暦である。つまり、1年を365.25日とするものである。なおこのとき、7月を自分の名前をとってユリウス月(英語:July)とした。
さらにローマ皇帝アウグストゥスは8年に暦の改訂を行い、8月をアウグストゥス月(英語:August)とした。そのため、7を意味するseptがSeptemberの9月になり、8を意味するoctがOctoberの10月というようにずれてしまった。11月、12月もそうである。
ユリウス暦は太陽年(365.2422日)とはまだかなりの差がある。実際に1582年には春分が3月10日になってしまった。10日間ほどのずれを生じたわけだ。これは春分の日を中心に復活祭(イースター)を祝うキリスト教徒にとっては大問題である。そこで、こうしたずれが少なくなるように、当時のローマ教皇グレゴリオ13世が制定したのがグレゴリオ暦であり、今日世界の多くの国で使われている。日本は1873年にグレゴリオ暦を採用した。
日本標準時グループ:http://jjy.crl.go.jp/