
第17章 海水中の塩分とその起源(2)
4.海水中の塩分の起源
a.陽イオン
海水中の陽イオンは、おもに河川が溶かし込んで運んできた陸の岩石がその起源である。下の表は「地球進化論」(岩波地球惑星科学講座13、1998年1月)による。これについてはこちらも参照。
| 溶存イオン | 海水中の濃度(10-3mol・L-1)=A | 河川水中の濃度(10-3mol・L-1)=B | 平均滞留時間(106年) |
| Na+ | 479.0 | 0.315 | 55 |
| K+ | 54.3 | 0.036 | 10 |
| Mg2+ | 10.5 | 0.150 | 13 |
| Ca2+ | 10.4 | 0.367 | 1 |
むかし、海水の塩分の濃度は河川が運び込むイオンのために年々濃くなっている、だから海水中の塩分の濃度を河川水中の塩分の濃度で割ってやれば海水の年齢(さらには地球の年齢)を求めることができると考えた人がいた。所が、上の表からもわかるようにその値は、長いナトリウム(Na+)でも5500万年、短いカルシウム(Ca2+)だとわずか100万年でしかない。これはあまりにも短すぎるし、イオンによってその値が異なることもおかしい。
※ 平均滞留時間(t)は、1年間に海に流れ込む河川水の総量Frw(3.8×1016kg/年)、海水量Msw(1.4×1021kg)とすると、t=(A×Msw)÷(B×Frw)となる。
現在ではこの値はそれぞれのイオンが海水にとどまっている平均の時間(平均滞留時間)、つまり元素が入れ替わる時間と考えられている。これは、河川水に溶け込んできたイオンの量と同じだけの海水中のイオンの量が海水から取り除かれている(海底で沈殿している)ことを示している。こうした状態を平衡という。

海水中のそれぞれのイオンが平衡状態にあるということは、例えば貝殻の化石からも確かめられる。貝殻の主成分である炭酸カルシウム(CaCO3)のなかのカルシウム(Ca)は一部ストロンチウム(Sr)と置き換わるが、その比は海水中のSr/Ca比によっている。そして、数億年前から貝殻中のSr/Caの値は変化していない。これは海水中のSr/Caの値が変化していないことを示す。こうしたことから、海水中の各イオンそれぞれの比の値は過去数億年間は変化していないことがわかる。つまり、海水の組成は少なくとも貝殻化石が出てくる数億年前からあまり変化していないということになる。
海水中のイオンを供給するための火成岩の量と、こうして運ばれてきた物質からどのくらいの堆積岩ができるのかはこちらを参照。
b.陰イオン
陰イオンの起源は、火山ガスが海水に溶け込んだものである。火山ガスの主成分は水蒸気(H2O)である。ほかに二酸化炭素(CO2)、硫化水素(H2S、火山・温泉に特有な匂い)、二酸化イオウ(SO2)、塩化水素(HCl)、フッ化水素(HF)、水素(H2)、窒素(N2)、アルゴン(Ar)、メタン(CH4)、一酸化炭素(CO)などが含まれる。
主成分の水蒸気(H2O)は冷えて水(つまり海水)となり、その水に水に溶けやすい火山ガスが溶け込んで海水中の陰イオンとなる。これだけだと強酸性の海水になってしまうが、その酸性の海水は岩石を溶かすことによって速やかに中和されて、今日の姿になっていく。いったん平衡に達すると、あとは長い間その状態を続けることになる。生命が発生したころの海水の組成は、すでに今日のものとあまり変わっていない可能性が高い。海水の変遷についてはこちらも参照。
C.まとめ
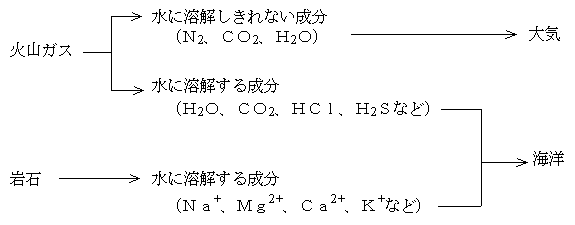
下図のように火山ガスの主成分が冷えて水(海水)ができると、水に溶けにくい成分が残って大気となる。地球大気の主成分が水に溶けにくい窒素であるのはこうして説明できる。二酸化炭素や水蒸気の一部は大気に残る。
一方、火山ガスのうち水に溶けやすい成分は海水に溶けて、陰イオンとなる。また陸の岩石が侵食されて陽イオンを供給する。
大気と海水の起源についてはこちらも参照。
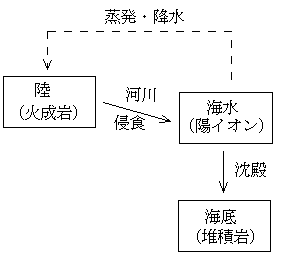
堆積岩をつくるための火成岩の量:陸の岩石(火成岩=Xkg)が侵食されて、海水1kg中のあるイオンを供給し、またそのイオンが沈殿して海底で堆積岩(Ykg)に含まれるようになったとする(下図)。例えば、上の表でナトリウム(Na+)とカリウム(K+)を供給するのに必要な陸の岩石(火成岩Xkg)と、海底で堆積してできる岩石(堆積岩Ykg)を求めてみる。
上の表をそれぞれの1kgに含まれる質量比(%)に換算して、下の表を得る。
| 岩石・海水中の質量比(%) | |||
| 火成岩(Xkg) | 海水(1.0kg) | 堆積岩(Ykg) | |
| ナトリウム(Na+) | 2.8 | 0.997 | 0.97 |
| カリウム(K+) | 2.5 | 0.0369 | 2.7 |
ここから
ナトリウム(Na+) → 0.028×X=0.997×1.0+0.0097×Y
カリウム(K+) → 0.025×X=0.000369×1.0+0.27×Y
これを解いて、X=0.52(kg)、Y=0.47(kg)となる。つまり、陸の岩石0.52kgが侵食されて、海水1kg中のナトリウム(Na+)やカリウム(K+)が供給され、また堆積岩0.47kgが海底で堆積してできるということになる。
これはいいのだが、他のイオンの組み合わせと使うと、XやYが違う値になってしまう。この場合は贅沢な悩みで、未知数が二つ(X、Y)なのに、方程式がイオンの数だけできてしまうということになる(ふつうは方程式の数より未知数の数の方が多い場合が多い、例えば地球内部の密度の求め方参照)。実際には、たくさんの方程式を使ってできるだけもっともらしい値を出すことになる。