
第2章 地球の形と大きさ
1. 地球の形
| 目次 | |
| a. | 地球の形(1) |
| b. | 地球の大きさ(1) |
| c. | 地球の形と大きさ(2) |
| d. | ジオイド |
| 用語と補足説明 | |
| このページの参考になるサイト | |
a.地球の形(1)
地球は丸い。このことは古代ギリシャの人たちも知っていた。船で沖から陸に近づくとき、遠くではまず小さな山の頂から見え始めて、裾野は陸に近づいてこないと見えない。あるいは北極星の高度が北に行くほど大きくなることもある。こうしたことから地球は平ではないとわかる。
アリストテレス(紀元前384年〜322年、子供の頃のアレクサンドロス大王(紀元前356年〜323年)の家庭教師もやったことがある)はさらに、月食は地球の影の中に月が入ることによって生ずる現象であること、その影の縁の形がいつも丸いということから、地球は球であると確信した。
さらに時代を下り、マゼラン(1480年ころ〜1521年)は1519年9月20日にポルトガルから出発し、西回りで世界一周を果たし、1522年9月6日にポルトガルに戻った。もっとも、マゼラン自身は1521年4月にフィリピンでの現地の争いに巻き込まれて死んでいる。出発時の237名中、生還できたのはわずか18名という苦しい航海であった。航海日誌の日付と、戻ってきたときのポルトガルの日付が1日ずれていたという。まさに地球が丸いことの証拠である。なお、これについては日付変更線を参照。
現在では、宇宙から地球を見ることもできる。こうした写真を見れば地球の形が球であることが実感できる。

アポロ17号から見た地球:NSSDC Photo Gallery
http://nssdc.gsfc.nasa.gov/image/planetary/earth/apollo17_earth.jpg
b. 地球の大きさ(1)
アレクサンドロス大王は、ペルシャ、エジプトなどを支配下におき、空前の大帝国を建設した。そして各地に彼の名を冠したアレクサンドリアという都市を建設した。アレクサンドロス大王の死後、彼の帝国は分裂する。そのうち、エジプトで彼の帝国を引き継いだのはプトレマイオス王朝である。そのエジプトのアレクサンドリアは空前の繁栄を誇る。
プトレマイオス王朝は、このアレクサンドリアに巨大な図書館を作った。そこで働いていたのがエラトステネス(紀元前276年ころ〜196年ころ)である。上のような事情で、エジプトに住んでいたがギリシャ人である。彼は夏至に日に、アレクサンドリアのたまたま真南(ほぼま南)にあるシエネ(今のアスワン)という町では、井戸の底まで太陽の光が差し込むということを知った。つまり、この日、太陽の南中高度が90°になるということを知った。いまでいうと、シエネは北回帰線上(ほぼ北回帰線上)の町ということになる。
この夏至の日、エラトステネスが住んでいるアレクサンドリアでは、太陽の南中高度は82.8°(鉛直方向に対し7.2°)であった。非常に遠い太陽からの光は地球上では平行光線になっていると考えると、この7.2°は、アレクサンドリアとシエネの緯度の差(経度は同じ)ということになる。
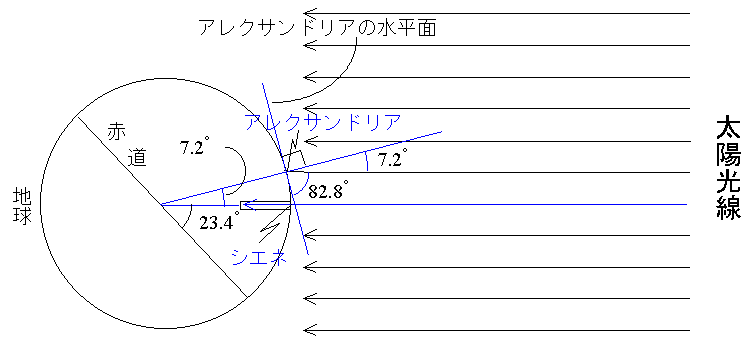
あとはアレクサンドリアとシエネの距離がわかればよい。ただ当時、これは難しい問題だった。エラトステネスは両都市間の距離を、旅人の旅程から求めた。それによると両都市の距離は、当時の長さの単位で5000スタジアになる。1スタジア185mといわれているので、5000スタジア=925kmとなる。
アレクサンドリア−シエネ間の距離/地球の全周=7.2°/360°だから、地球の全周は46500kmと計算される。本当の地球の全周は40000kmなので、2000年以上も前ということを考えると、驚くべき精度で地球の大きさが求まっていたことになる。
現在では、高精度のGPS(グローバル・ポジショニング・システム)が使える。離れた南北間の距離を実測し(直接測れる距離なら直接、それよりも遠ければ地図で)、両端の緯度をGPSで求めれば、エラトステネスの方法が使える。
もう一つ、国土地理院の2万5千分の1地図閲覧システム(試験公開中)を用いる方法もある。
http://watchizu.gsi.go.jp/
ある地点をクリックすると緯度・経度の値が得られる。だから南北の2地点を選んでそれぞれの緯度を求め、その2地点の距離を地形図上から測って、上のエラトステネスの方法を用いるということもできる。
では、地球が丸いとすると地平線(水平線)は何km先が見えているのだろう。下の図のように、半径R(6400km=6.4×106m)の地球上で高さhm(緑線)で見る。x(赤線)が求める距離となる。
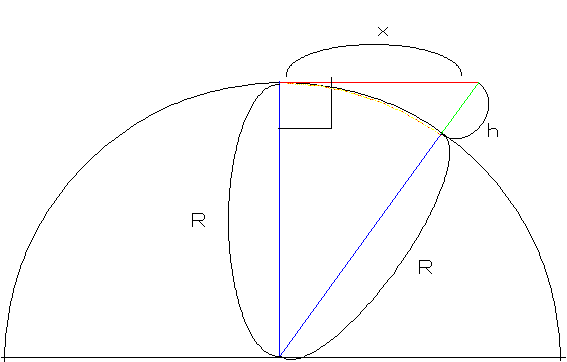
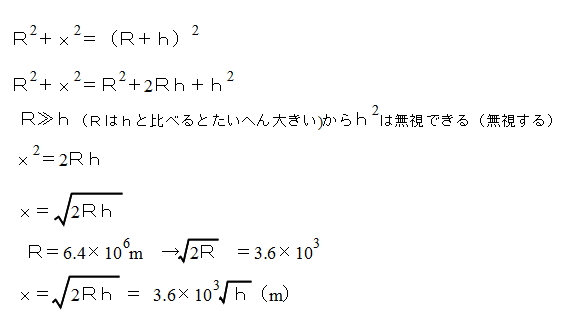
つまり、見える距離(km)は目の高さ(m)の平方根に比例し、距離の単位をkm、目の高さの単位をmとすると、比例定数は3.6である。目の高さが1mの人は3.6km先が地平線(水平線)ということになる。目の高さが1.5mの人だと、4.4kmくらいとなる。100mの山では10倍の距離の約36km先が地平線(水平線)。富士山(約3800m)では約220km先が見えることになる。だから富士山は、富士山から220kmの範囲のところなら見えるはずである。もちろん、これは海抜0mでの話で、高いところに登ればもっと遠くから富士山は見える。
※ 実際は空気の屈折のためにもう少し先まで見える。空気の屈性を考えたとき、上の式の比例定数は3.9程度になる。
800mの高さでは約100km先まで見える。逆に富士山から約100km離れた東京からは、富士山の800m以上の高さだけが見えることになる。
西の海に沈む太陽を、海抜1m(目の高さ)で見る。太陽の上端が水平線に沈んだ瞬間、4mの高さの見晴台にいる人はどうだろう。4の平方根は2だから、その人が見ている水平線までの距離は2倍になる。3.6×2(m)=7.2km、つまり7.2km先まで見える。これは高さ1mよりも約3.6km先である。地球の円周と比べてこの値は小さいので、この長さが地球の円周の一部(弧)と等しいと考えると(上図の赤い直線と黄色い弧の長さが等しい)、また太陽が水平線に直角に沈んだとすると、北緯35度で地球が3.6km自転するのに要する時間は約8秒だから(1秒で、4万km÷(24×60×60)=0.46km、3.6kmはその8.0倍)、日没が約8秒遅れることになる。
太陽が沈むところを見るチャンスがあったら、しゃがんで見ていて沈んだ瞬間に立ち上がる(ジャンプしてもよい)と再び太陽が見えるはずである。このようにしても、地球が丸いことが実感できる。例えば、しゃがみ込んで50cmの高さから見ていて、立ち上がったとき1.5mの高さになったとすると、見える水平線までの距離の差は3.6(√1.5-√0.5)km=1.9km。1.9km自転するに要する時間は4.4秒。
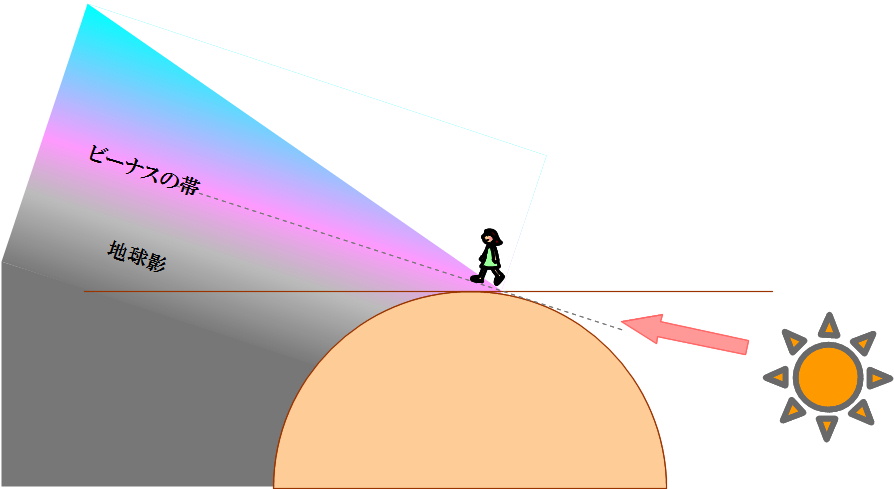
地球が丸いため、空に映る地球の影が見えることがある。またその影の上は薄いピンクの帯になっていて、「ビーナスの帯」と呼ばれている。
 |
 |
| 地球影 | 南米ボリビアのウユニ塩湖で見た地球影(2012年8月15日撮影) |
ニュートン(イギリス、1642年〜1727年)は自分の理論が正しいとすると、自転による遠心力のために、赤道方向に膨らんだ回転だ円体(だ円をその軸を軸として回転させたときにできる形)になっているはずだと考えた。そして、もし地球の全体が密度一定の液体なら、その扁平率は1/230だろうと予想した。
一方ホイへンス(オランダ、1629年〜1695年)は、地球の質量がすべてその中心(重心)に集まっているなら、扁平率は1/578と予想した。
またカッシーニ(イタリア→フランス、1625年〜1712年、パリ天文台初代台長、土星の環のすき間(カッシーニの間隙)を発見したりした。最後までニュートンの万有引力の法則を認めなかった。光速が有限であることも認めなかった。)は、ニュートンたちとは逆に、地球は北極−南極方向に伸びた回転だ円体であると主張した。
どちらが正しいのかを決めるには、図のようにニュートンたちが主張しているように(当時はまだニュートン力学を認めない人たちもいた)、赤道方向に膨らんだ形をしているなら、赤道の丸みに合わせた円よりも、極の丸みに合わせた円の方が大きくなるはずである。具体的には、同じ緯度の差に対する経線の長さを比べて、弧AB>弧CDとなることを確かめればよい。
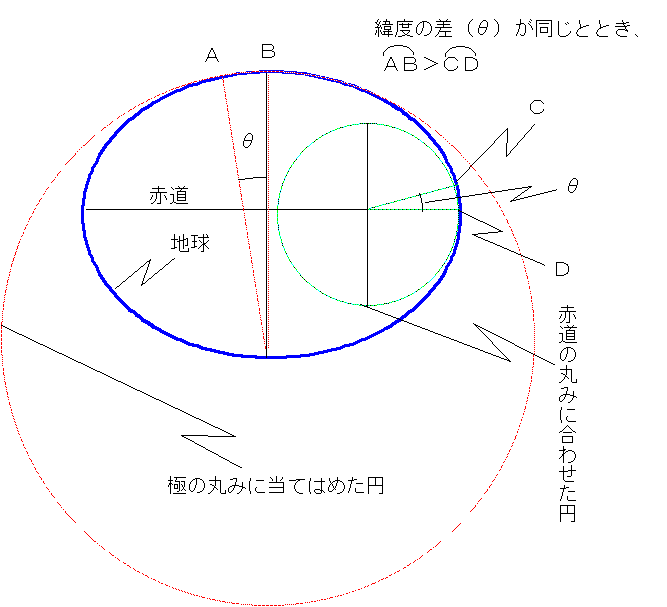
そこでフランスの学士院は、(フランスのカッシーニの考えの方が正しいことを証明しようと)高緯度では1736年にスカンジナビア半島のラプランド地方に、一方低緯度では1735年に南米のペルーに測量隊(ブーゲたち)を送った。ラプランド隊はその年のうちに測量を終わったが、ペルー隊は大変であった。アンデス山脈の数千メートルの高地、道もないようなところで測量しなくてはならない。結局7年9か月かかり、1743年にようやく測量が終わった。
結果はフランスの期待に反して、ニュートンたちの予想通り、緯度の差1°に対する経線の長さはラプランド地方の方が、ペルー地方より長かった。これは、ニュートンの力学が正しいことを示したことにもなる。このようなところからも、ニュートン力学が確固たる地位を築くことになる。
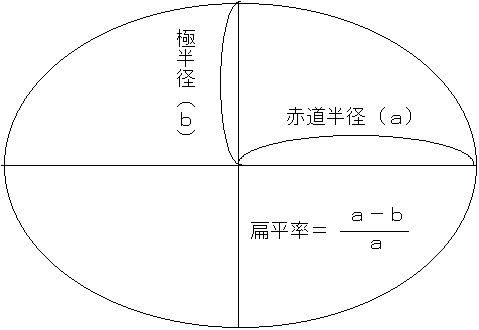
実際の地球の形に最も近い回転だ円体を、地球だ円体という。最新の測量結果を反映した現在(1999年)の地球だ円体の値は、赤道半径(a)=6378137m 扁平率=1/298.257222101 (極半径(b)=6356752m) となっている。つまり、赤道半径の方が極半径より約21385m(約21km)長いことになる。
地球の扁平率の値は、ニュートンやホイヘンスが予想した扁平率の間の値になっている。これはもちろん、地球は密度一定の液体でもないし、質量が中心に集まっているわけでもない、まさにその間の状態だからである。そういう意味では、ニュートンやホイヘンスの予想は合っていたことにもなる。
d.ジオイド
地球の形とは何だろう。海では平均海水面がそれであることは簡単に理解できる。平均海水面とは、潮汐や波など全部を平均した海水面ということである。平均海水面は重力の向き(鉛直線)に垂直な面(のうちの一つ)である。なお、重力についてはこちらを参照。
では、地形の凹凸のある陸ではどうすればいいのだろう。ここで、もし陸に縦横無尽に溝を掘り、その溝に海水を引き入れたら、平均海水面の延長ができる。そのときその「平均海水面」はどうなっているのだろう。上に書いたように、平均海水面は重力に垂直である。そこで、重力が働く向きを考える。
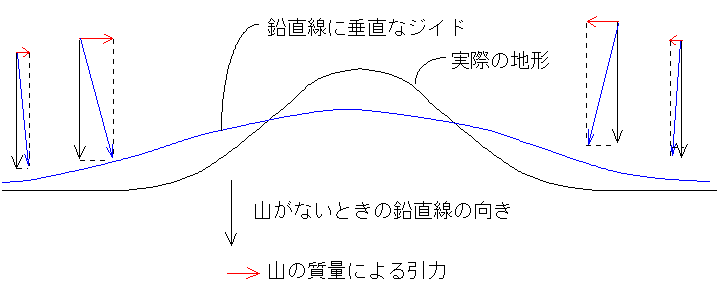
陸(山)の質量による引力(質量があれば引力が生ずる=万有引力の法則)が、山の向きに生ずる。だから、山がない場合の鉛直線の向きよりも、山寄りに鉛直線の向きが変わってしまう(図の青色の矢印)。平均海水面は鉛直線に垂直だから、山の近くだと水平面が図のように「傾く」(もちろんこれが水平面であるが)ことになる。これがジオイド面であり、ジオイド面は陸では少し盛り上がることになる。
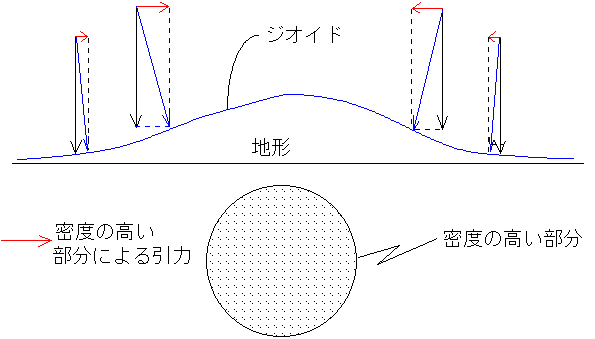
地下に密度の高い物質があると、それだけ引力(引力は質量の積に比例する)がまわりより強くなる。だからその近くでも、ジオイド面が盛り上がる。
現在では、人工衛星の飛び方を詳しく解析することにより、ジオイド面が正確に求まる。地球だ円体とは、ジオイド面に最も近い回転だ円体をいう。ジオイドで見ると、地球はジャガイモ型といいたくなるような形をしている。
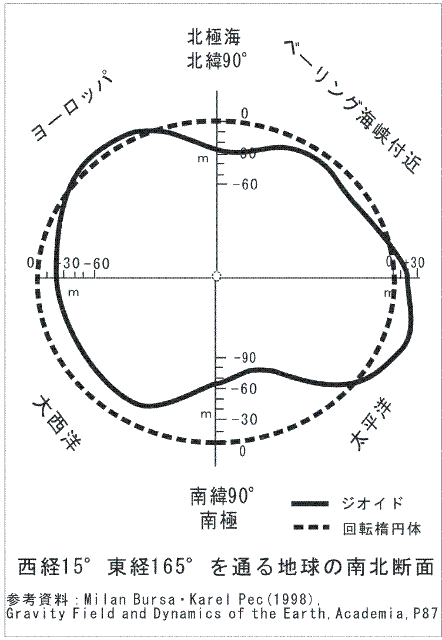 |
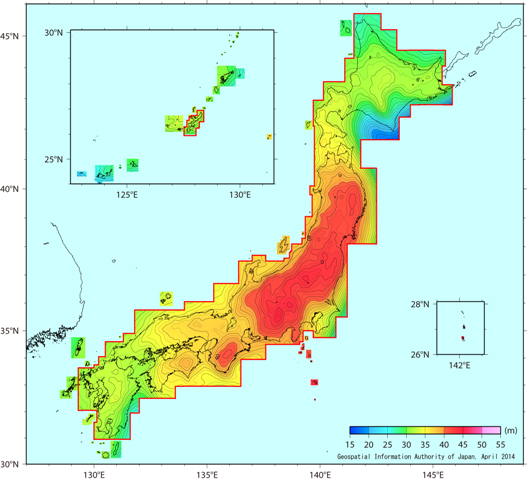 |
| 国土地理院:http://vldb.gsi.go.jp/sokuchi/geoid/geoid.html | 日本のジオイド面:国土地理院http://www.gsi.go.jp/buturisokuchi/buturisokuchi40004.html |
また、正確には標高(海抜高度)はジオイド面からの高さをいう。日本では東京湾の平均海水面を海抜0mとしている。ただし、実際には東京都千代田区永田町1-1国会議事堂前庭北地区内(憲政記念館構内)に水準原点(24.4140m)を設け、それを基準に標高を測っている。
※ 2011年3月11日に起きた東北地方太平洋沖地震による地殻変動のため、水準原点は2011年10月21日に24.3900mと改定された。この高さは、神奈川県三崎の油壺験潮場(の潮位)と水準原点と間の水準測量によるものである。今後も定期的にこの測量が行われる予定である。つまり、実際には油壺での平均海水面が基準となっている。
※ 地球の中心からの距離を山の高さとすると、赤道近くの高い山の方がエベレストよりも高いことになる。下を参照。
海ではジオイド面と平均海水面は一致していて、地球だ円体はその上を通る。陸では一般に、ジオイド面−地球だ円体−地表の順に高くなる。
プトレマイオス王朝:プトレマイオス王朝の最後がクレオパトラ(クレオパトラ7世、紀元前69年〜紀元前30年)である。プトレマイオス王朝はエジプトにあるが、アレクサンドロス大王が築いた帝国の流れを引いているので、支配階級はギリシャ人である。エジプトの地にあって、王家の血筋を守るためとも、統治のために支持を集めるため現地の風習を取り入れたともいわれているが、兄弟姉妹で結婚する風習があった。クレオパトラの夫は5歳年下の弟であるプトレマイオス13世である。しかし、姉弟が不仲になり、闘争を始める。一時は弟に追われたクレオパトラだったが、エジプトに侵攻してきたカエザル(シーザー、紀元前100年〜紀元前44年)に取り入り女王になる。その後カエザルに従ってローマに渡り、彼が暗殺された後はアントニウス(紀元前88年ころ〜紀元前30年)に取り入る。しかし、アントニウスの失脚に伴い、アレクサンドリアに戻り自殺する。
地球の全周:1mという長さは、もともとは北極からパリを通り赤道までの距離の1000万分の1と決められた。これがメートル法のはじまりである。だから、北極−赤道の距離は10000000m(107m)、つまり1万km(104km)となる。これは地球の全周の1/4だから全周は4×104kkm(4万km)。
その後幾度かの変遷を経て、現在の1mの定義は、「光が真空中で(1/299792458)sの間に進む距離」となっている。1m定義も変わってしまったし、また地球自体が完全な球でないので、地球の全周は正確に4万kmではないが、もともとの定義から、全周は約4万kmであることにかわりはない。
メートル法:フランスでは、フランス革命(1789年)により合理的な精神が高まり、長さも人の手足を基準とした単位(フィートなど)ではなく、科学的な単位を制定しようという気運が高まった。そして、上に書いたように。北極からパリを通り赤道までの距離の1000万分の1を1mと決めた。
実際には、フランス国内(ダンケルク(51.00°N、2.38°E)からパリを通って、ダンケルクのほぼ真南のスペインのバルセロナ(41.25°N、2.08°E)まで)の長さを正確に(当時としては)測量して、地球の大きさを求めた。そして、1795年にメートル法を定めた。こうした歴史もあり、フランスはメートル法を早くから取り入れた。
※ このダンケルク−バルセロナ間の測量については「万物の尺度を求めて」(早川書房、2006年)に詳しい。この測量も大変だったようだ。
一方イギリスは、フランスに従うのを由としない風潮があった。しかし、子午線の基準(経度0°)をグリニッジ天文台を通る子午線という主張を通す代わりに(フランスは当然パリ天文台を通る子午線を経度0°と主張した)、長さでは譲ってメートル法を採用することにした(1875年)。しかし、実際にイギリスがメートル法を採用するのは1974年になってである。だから、まだ長さでもフィートやヤードという単位がよく使われている。
メートル条約に加盟した国には、白金とイリジウムを9:1の割合で混ぜた合金作った「メートル原器」が配られた。日本は1885年にメートル条約に加盟したが、完全実施は1966年である。
なお、単位の項も参照。
地球の中心からの距離:地球の中心からの距離(地心距離)ベスト10は下の表の通り。ちなみ北緯27°59′にあるエベレスト(標高8848m)は32位(地心距離6382.270m)。また地心距離では、北緯35°21.6′にある富士山(標高3776m、地心距離6374.488m)より、北緯20°25.2′にある沖ノ鳥島(標高0m、地心距離6375.595m)の方が高いことになる。北緯30°20.2′にある屋久島の宮之浦岳(標高1935m、地心距離6374.4631m)は富士山とほとんど同じになる。さらに世界で一番深いマリアナ海溝のチャレンジャー海淵(北緯11°19′、標高-10920m、地心距離6366.324m)は、北極海海底(北緯78°46′、標高-5608、地心距離6352.000)よりも“浅い”ことになる。
| 山名(国) | 緯度 | 標高(m) | 地心距離(km) | |
| 1 | チンボラソ(エクアドル) | 1°29′S | 6310 | 6384.458 |
| 2 | ワスカラン(ペルー) | 9°08′S | 6768 | 6384.397 |
| 3 | イェルパハ(ペルー) | 10°16′S | 6634 | 6384.125 |
| 4 | コトパクシ(エクアドル) | 0°40′S | 5896 | 6384.054 |
| 5 | キリマンジャロ(タンザニア) | 3°05′S | 5895 | 6383.952 |
| 6 | カヤンベ(エクアドル) | 0°02′S | 5790 | 6383.947 |
| 7 | アンティサナ(エクアドル) | 0°30′S | 5704 | 6383.860 |
| 8 | ウイラ(コロンビア) | 3°00′N | 5750 | 6383.855 |
| 9 | チャンパラ(ペルー) | 8°37′S | 5753 | 6383.435 |
| 10 | イリニザ(エクアドル) | 0°40′S | 5363 | 6382.270 |
「地球が丸いってほんとうですか」(日本測地学会監修、大久保修平編著、朝日新聞社)より作成。
ペルー(現エクアドル)の測量隊:観測を担う中心の隊員は優秀な数学者ピエール・ブーゲ(ブーゲー、ブーゲ異常に名を残す、1698年〜1758年、当時37歳)、探検家に憧れる数学者シャルル=マリー・ド・ラ・コンダミーヌ(1701年〜1774年、当時34歳)、数学&天文学者ジャン・ゴダン(1704年〜1760年、当時31歳)だった。観測隊はトラブル続きだった。それは技術的な問題ばかりではない。
1735年5月出航。まず、目的地の途中、カリブ海の現在のドミニカのサント・ドミンゴに停泊中(当時のペールはスペインの植民地だったので、そのスペインの許可が出るのを待っていた)、ジャン・ゴダンが現地の女性との恋愛沙汰で公金(測量費)を使い込んでしまった(ダイヤモンドのプレゼント、現在の価値で490万円ほど)。以後、測量隊は費用不足に悩むことになり、また当然ゴダンとは仲違いとなる。
1736年3月にペルーに到着しても資金が足りない。そこで、まずエクアドルの首都キトに行くことにする。地元の権力者たちに資金援助を頼むためである。そのキトまでも冒険だった。地図のないジャングルを進まなくてはならなかったのだ。3人は別々にキトを目指すことになった。ゴダンは地元のガイドとともに進み、ブーゲはその後をつけることになった。コンダミーヌは一人でジャングルを横断することになった。
コンダミーヌはそのジャングルの中で、地元のケチュア族が利用していたゴムの木を見つけ、ゴムの木の種子を本国に送る。その後のジャングル行は大変だった。ガイドにも逃げられ、方向を失い、ようやくバナナで命をつなぐ有様となる。さらには高熱を出してしまう。奇跡的に熱が下がったコンダミーヌは山頂からキトを見つける。
ゴダンとブーゲはコンダミーヌよりも先にキトに着くがお金がない。キトの有力者エルサドに資金援助を頼むが断られてしまう。社会的地位が上のコンダミーヌによる説得を期待して、彼の到着を待つしかない。しかし、遅れて到着したコンダミーヌはホテルの部屋にこもったままになってしまう。有力者エルサドに会うための服がなかったという理由で。1週間後、ようやく服装を整え、エルサドに会ったが援助は得られなかった。その代わりエウサドはコンダミーヌの持ち物を売る権利を与えた。当然それはそれほどの資金にはならない。こうしたことから、フランスを出航してから18ヶ月間、測量を始めることができなかった。
それでも、不十分な資金で測量を始めることになった。赤道を目指し、ジャングルに入ったところ最年少の隊員ククルが病(マラリア?)に倒れ死んでしまう。コンダミーヌは資金調達のために再び一人でジャングルを横断し、ペルーの首都リマを目指す。その途中で、マラリアの特効薬キニーネについての重要な発見をする。キナの木には白い皮、黄色い皮と赤い皮などの違いがあり、赤い皮の種類が薬になることをペルーの人は知っていて、コンダミーヌもそれを教えてもらったのだ。当時のヨーロッパではこの種類の違いが知られておらず、キニーネには効くものと効かないものがあるという程度の知識、またそれが悪徳商人の儲け(皮の色の種類の違いを混ぜて売る)にもなっていた。外交センスがあったのか、コンダミーヌはリマで資金(12,000ペソ、約4,900万円)を調達できた。
ようやく資金を得た測量隊は、赤道から測量を始める。でも、ここからも大変だった。高山病に悩みながら、4000mクラスのアンデス山脈を登らなくてはならなかった。焼けるような暑さや厳しい寒さの中での計測、その上測量機器を地元民に盗まれたり、ガイドに逃げられたりということもあった。また、山頂では測量可能な天気に恵まれるまで数日どころか、1ヵ月も待たなければならないこともあった。でも、チームが仲直りをしたわけではない。ブーゲ&コンダミーヌとゴダンに分かれて行動することになった。この測量の過程で、コンダミームはメートル法のアイデアを思いついたといわれている。そして、ブーゲはで山の重力が標準重力よりも小さいというブーゲ異常を見つけた。
測量をほぼ終えた頃、エクアドルのクエンカ(クエンカの植民地時代の建築物は「サンタ・アナ・デ・ロス・リオス・デ・クエンカの歴史地区」としてユネスコの世界遺産に指定された(1999年))という町でまたトラブルを起こしてしまう。闘牛に招待された測量チームの中の医者が、婚約者のいる女性と仲良く闘牛場に現れてしまったのだ。観衆の怒りを買ったチームは地元の人たちに襲われてしまい、結局医者は逃げる途中で刺されて死んでしまう。ブーゲは刺されながらも助かった。
当初3年の予定だった測量は、丸8年かかってしまった。しかし、この結果地球の正確な形が分かったのだ。つまり、ニュートンが提唱した赤道方向に張り出した回転だ円体ということを明らかにしたのだ(フランスのカッシーニが間違っていたことも)。
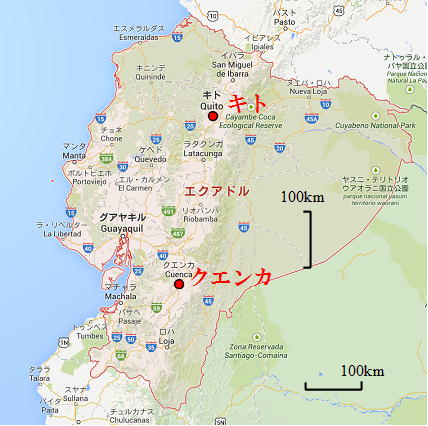
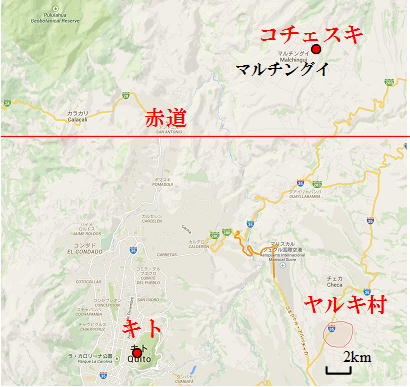
※ 実際の測量は、1737年10月にまずキト郊外のヤルキ平原で基線の測量(実測)から始まった(下の記念切手参照)。6500トワーズ(約13km)の長さを平らにし(灌木を引き抜き、木々を伐採し、巨大な岩を動かし、溝を埋め、壁があれば穴を開け、1つだけあった小川には木の橋を渡し、動かせない岩は爆破し、草木が密生しているところは燃やして)、1メートルごとに杭を立て、基線がまっすぐであることを照準器で確認する。次に3本の木の竿(定規)を順につないで実測する。これのほぼ1ヶ月かかった。そしてこれをもとに、キトの北コチェスキからクエンカの南タルキまでの緯度差約3°(平均緯度は南緯約1°30′)の間を三角測量した。(1辺の両端から目標(頂点)を見込む角度を測定して、三角形を決定する。この三角形をつないでいく。下の記念切手参照)。タルキの測量を終えたのは1740年12月、三角形は43(角度の測定は129)、観測緯度地点は43、全長345kmだった。これで終わりではない。こんどはクエンカ近郊で基線を作り測量する。ついで、南端と北端での天体観測を行い両地点の正確な緯度を求める。これにも3年かかった。キトとコチェスキ、クエンカとタルキの位置は下の地図を参照。
(参考図書「地球を測った男たち」(フロランス・トリストラム、喜多迅鷹・デルマス柚紀子訳、Libro、1983年、ISBN4-8457-0097-2))
もっとも、測量が終わってもフランスに帰国する十分な費用もない。結局1743年、一人先にブーゲだけが先に帰国した。ブーゲは帰国後、ブーゲ異常を発表し、また造船工学の道に入った。
コンダミーヌはジャングルの探検に戻り、フランスに戻ったのは1744年だった。そして彼は、アマゾン川とオリノコ川をつなぐカシキアレ川や、アマゾン原住民の使う矢毒(クラーレ)の報告をすることになる。ゴダンはしばらくリマ大学の教授を務めた後帰国し、スペイン、カディスの海軍大学の校長になった。
 |
||
| 写真:エクアドルの記念切手 1986年フランス遠征隊によるペルー方面(現エクアドル)子午線長測定250年、左上は1736年コンダミーヌ測量隊による赤道附近の子午線長測定時の三角網図、右上はフリッツ(Samuel Fritz 1654〜1728、ボヘミア生まれのジェスイット派修道士)によるマラニョン川、アマゾン川源流の地図、コンダミーヌはこの地図の多くの誤りを修正、下はキト近傍ヤルキ(Yarouqui)平原の基線風景 http://uenishi.on.coocan.jp/50lib-stamp/814stampD-F.html |
||
 |
 |
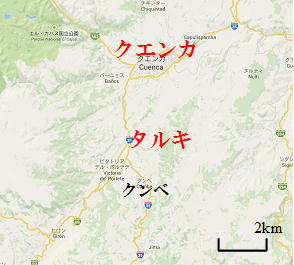 |
| 測量を行ったキトからクエンカまで(現エクアドル) | 基線を測量したヤルキ、測量の北端コチェスキ | 測量の南端タルキ |
| google mapに加筆 | ||
日本測地学会の測地学テキスト:http://www.geod.jpn.org/web-text/