| このページの目次 | ||
| 第3章 太陽(3) | ||
| 3.太陽のエネルギー | ||
| a.太陽定数 | ||
| b.太陽の全放射エネルギー | ||
| c.太陽表面1m2あたりの放射エネルギー | ||
| d.太陽質量1kgあたりの放射エネルギー | ||
| 4.太陽の表面温度 | ||
| 用語と補足説明 | ||
| 参考になるサイト | ||
3.太陽のエネルギー
a.太陽定数
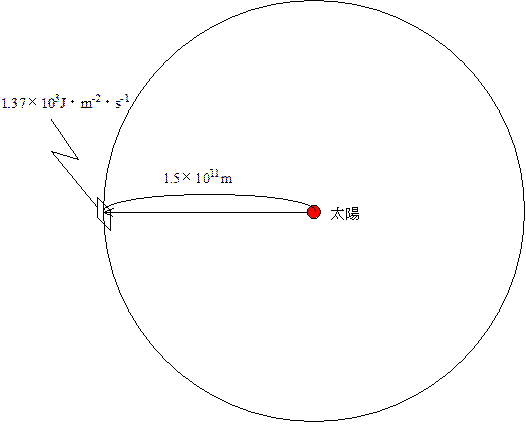
太陽から地球に送られてくるエネルギーを正確に測定するためには、地球の大気による吸収・反射の影響を避けるために大気圏外で測定しなくてはならない。大気圏外で、太陽光線に対して垂直な1m2の面が1秒間に受けるエネルギー(J)を太陽定数という。
太陽定数=1.37×103J・m-2・s-1
J・s-1はW(ワット、仕事率)であるし、103はk(キロ)であるので 太陽定数=1.37kW・m-2ともかける。
この太陽定数は、太陽のエネルギーとそれをもとにした議論をするためには大切な値であるが、人工衛星によって大気圏外で太陽エネルギーを測定できる今日でも、その精密な測定は難しい。
太陽は地球に向かってだけエネルギーを送っているのではなく、宇宙のあらゆる方向に対して同じようにエネルギーを放射していると考えられる。つまり、太陽から1.5×1011m(太陽と地球の距離)離れ、太陽光線に対して垂直な1m2には、太陽定数と同じエネルギーが来ているはずである。つまり太陽を中心として、半径1.5×1011mの球の全球面が受けている全エネルギーが、太陽が放射している全エネルギーであり、その1m2には太陽定数と同じエネルギーが来ている。
太陽の全放射エネルギー=(太陽定数)×(太陽−地球の距離を半径とする球の表面積)
→ 1.37×103J・m-2・s-1 = 3.85×1026J・s-1(約4×1026J・s-1)…(1)
この値が太陽のことを考える上での基礎的な数値である。

太陽の半径は6.960×108mなので、その表面積は4π×(6.96×108m)2。この値で(1)の値を割れば、太陽の表面1m2あたりの放射エネルギーが求まる。
その値は6.33×107J・m-2・s-1 …(2)
太陽の質量は1.989×1030kg(約2.0×1030kg)なので、(1)の値をこれで割れば、太陽の質量1kgが毎秒放出しているエネルギーが求まる。
太陽の質量1kgあたりの放射エネルギー = 2×10-4J・s-1・kg-1 …(3)
4.太陽の表面温度
太陽の表面温度は、物体(厳密には黒体)が放射するエネルギーは、その物体の温度(絶対温度)の4乗に比例するという、ステファン・ボルツマンの法則から求めることができる。放射エネルギーE(J)、物体の温度T(K)とすると、を
E=σT4 ここでσ(シグマ)はステンファン・ボルツマン定数(5.67×10-8(J・s-1・m-2・K-4))
太陽の1m2あたりの放射エネルギー(6.33×107J・m-2・s-1)を上式に代入してTを求める。こうして求められたTを有効温度といい、その値は5770K(ケルビン)である。この値はおおよそ6000℃である。
太陽の表面温度:太陽の表面温度は、上のステンファン・ボルツマンの法則以外にも、ウィーンの変位則からも求めることができる。ウィーンの変位則については、こちらやこちらを参照。太陽の放射エネルギーの中で最大強度の波長は0.46μmなので、下のλmaxにこの値を代入して太陽の表面温度を求める。
λmax・K=2900 λmax(ラムダ・マックス):最大強度の光の波長(μm) T:表面温度(K)
こうして求められた太陽の表面温度は6300Kとなる。
ウィーンの変位則から求めた温度とステンファン・ボルツマンの法則から求めた温度(有効温度)が一致しないのは、太陽の大気による吸収や、太陽が厳密には黒体ではないためである。だから、太陽の表面温度は6000K、あるいは6000℃といってもよい。