1=100、10=101、100=102、1000=103、10000=104という具合に、大きな数になっていくと10の何乗という指数表示が便利である。さらに、大きな数を見かけ上小さな数として表わすのが対数である。とくに10の何乗の部分の数値を常用対数という(10を底とする対数)。ふつう(理科では)対数といえば、常用対数を指す。
対数(記号は“log”)を使うと、log1=0、log10=1、log100=2,log1000=3、log10000=4となる。
では、2、3、4、…などはどうなるのだろう。じつは2=100.3010、3=100.4771、4=100.6020、5=100.6990、6=100.7782、7=100.8451、8=100.9030、9=100.9542などと表わすことができる。だから、log2=0.3010、log3=0.4771、log4=0.6020、log5=0.6990、log6=0.7782、log7=0.8451、log8=0.9030、log9=0.9542となる。
ここで、10x×10y=10x+yを思い出すと、この式の両辺の対数をとって、log10x×10y=log10x+y=log10x+log10y=x+yとなる。つまりかけ算(割り算)が足し算(引き算)になることがわかる。電卓やパソコンがなかった時代、大きな数の計算はこのように対数を利用していた。
このことから、log6=log(2×3)=log2+log3、あるいはlog5=log(10÷2)=log10-log2であることがわかる。本当にそうなっているか、上の数値で試してみよう。だから、log2、log3、log7の値さえわかれば、他のlog4、log5、log6、log8、log9の値はこのような計算で求めることができる。
また、log4=log(2×2)=log2+log2=2log2。これは、log4=log22=2log2。同じように、log8=log(2×2×2)=3log2。これはlog8=log23=3log2。このようにべき乗の対数は、べき乗の数値倍になる。
log2=log(√2)2=2log(√2) → log(√2)=(1/2)×log2)/2。さらに(1/2)×log2=log21/2。このように、平方根は1/2乗、立方根は1/3乗である。対数の表があれば、平方根や立方根も求めることができる。例えば、8の立方根は、log8=0.9030だから、その1/3の0.3010に対応する数、すなわち2である。
さらにlog2000=log(2×1000)=log2+log1000=3.3010である。この整数部分を指標(標数)、小数部分を仮数という。指標部分の数値で、その数の大きさ(桁数)がわかる。この場合の指標は3、つまり103(1000)のオーダーであることがわかる。
対数の表
| 整数 | 少数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 0.000 | 0.041 | 0.079 | 0.114 | 0.146 | 0.176 | 0.204 | 0.230 | 0.255 | 0.279 | |
| 2 | 0.301 | 0.322 | 0.342 | 0.362 | 0.380 | 0.398 | 0.415 | 0.431 | 0.447 | 0.462 | |
| 3 | 0.477 | 0.491 | 0.505 | 0.519 | 0.531 | 0.544 | 0.556 | 0.568 | 0.580 | 0.591 | |
| 4 | 0.602 | 0.613 | 0.623 | 0.633 | 0.643 | 0.653 | 0.663 | 0.672 | 0.681 | 0.690 | |
| 5 | 0.699 | 0.708 | 0.716 | 0.724 | 0.732 | 0.740 | 0.748 | 0.756 | 0.763 | 0.771 | |
| 6 | 0.778 | 0.785 | 0.792 | 0.799 | 0.806 | 0.813 | 0.820 | 0.826 | 0.833 | 0.839 | |
| 7 | 0.845 | 0.851 | 0.857 | 0.863 | 0.869 | 0.875 | 0.881 | 0.886 | 0.892 | 0.898 | |
| 8 | 0.903 | 0.908 | 0.914 | 0.919 | 0.924 | 0.929 | 0.934 | 0.940 | 0.944 | 0.949 | |
| 9 | 0.954 | 0.959 | 0.964 | 0.968 | 0.973 | 0.978 | 0.982 | 0.987 | 0.991 | 0.996 |
表の見方:log3.5ならば整数部3、小数部5のが交点の値0.544となる。log63ならばlog(6.3×10)=log6.3+log(10)=0.792+1=1.792。また、log1900=log(1.9×103)=0.279+3=3.279。log0.00078=log(7.8×10-4)=0.892+(-4)=−3.108。
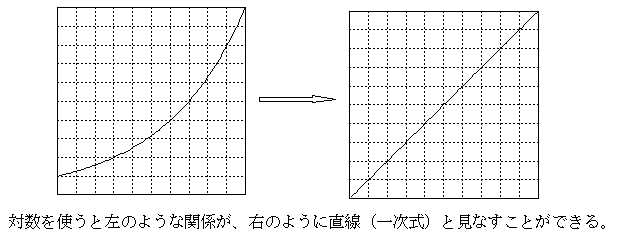
対数を使うと、指数関係であるy=10xという関係、つまりこの関数では、xが1から5になるとき、yは1、10、100、1000、10000、100000などと急激に増えていくが、対数をとる、つまりy=log(x)という関数にすれば、yは1、2、3、4、5とゆっくり増えていくばかりか、単純な直線関係(一次式)と見なすことできるので扱いが簡単になる。自然界ではこうした指数関係で変化するものが多いので、そうした場合対数をとると便利である。
