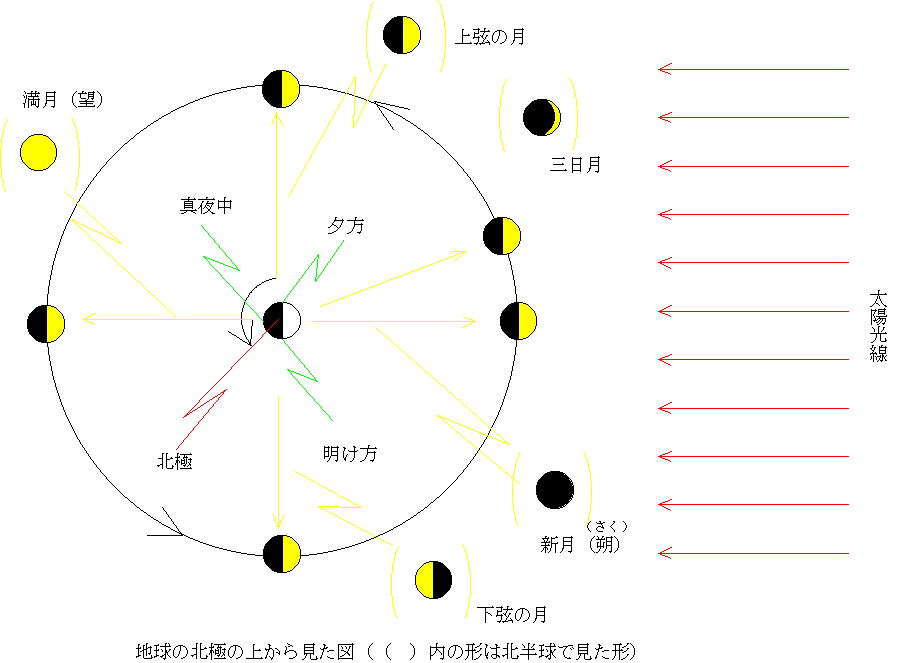
月は太陽の光を反射して光っている。その様子は下の通りであり、見かけの形は新月(朔(さく)ともいう)→上弦の月→満月(望ともいう)→下弦の月→新月(朔)を繰り返えして変化する。この周期は約30日であり、昔は月の満ち欠けを暦に利用していた。1月(ひとつき)がだいたい30日というのはその名残である。
月の出は1日で約51分ずつ遅くなる。新月から数えて3日目あたりの形が三日月であり、日が沈んだ後の西の空に見える。新月から数えて7日くらいで右半分(北半球)が見える上弦の月となる。このときの月は夕方ころに南中し、真夜中に西に沈む。新月から15日目あたりで満月となる。だから満月を15夜ともいう。満月のとき、月は太陽が西の空に沈むころ東の空に現れ、真夜中に南中する。さらに1週間ほどたつと、月の出はさらに遅れて夜半に東の空から昇ってくる下弦の月となる。そしてまた1週間ほどたつと(新月からは30日くらい)、再び新月に戻る。
上弦の月とか下弦と月という呼び名は、西の地平線に沈むときに弦を上にしているのか下にしているのかではなく、月の前半(上旬)に見える月か、後半(下旬)に見える月かという意味である。このときの弦は弓を振り絞ったときの形をいい、数学の用語としての弦(直線)とは少し意味が違う。また、新月のときの月は真っ暗でまったく見えないかというそうではなく、地球の反射光を浴びるためにうっすらと見える。
満月のときの明るさは、見かけの等級で-12.6等であり、見かけの等級-26.8等の太陽よりも約50万分の1の明るさとなる。それでも0等星よりも7万倍ほど明るい。満月のときの月の明るさから表面の反射率がわかる。その反射率は約7%で、地球の約40%、金星の約85%と比べると大変に小さい。これは、地球は宇宙から見ると表面は反射率の高い雲がかなりの面積を占めているし、極地の氷も反射率が高いし、海の反射率も大きいからである。金星は全体が反射率の高い雲におおわれている。一方、月には雲も氷もなく、反射率の低い岩石(砂)の表面が全部直接見えているからである。
日本には“中秋の明月”を愛でる風習がある(あった)。昔はススキと団子(お月見団子)を供えて、家族でその満月を見たものである。、“中秋”とは旧暦8月15日を指すが、現在、中秋の明月というと秋分の日にもっとも近い満月をいう。さらに細かいことをいうと、“仲秋”とは旧暦の8月のことである。

b.公転と自転
月はいつも同じ模様に見える(例えばウサギの餅つき)。つまり、月はいつも同じ面を地球に向けている。これは月は自転していないということではなく、月の自転周期と公転周期は同じだということである。ただし、厳密にいうと地球から見て絶対に見えないのは月の表面全体の41%、つねに見えている面も41%、残りの18%は見えたり見えなかったりする。
月は地球の公転・自転の向きと同じ向きに地球のまわりを回っている。その月の公転周期(=自転周期)は、ちょうど恒星日と太陽日の関係と同じく、何を基準にするのかということで二通り考えられる。一つは恒星を基準とした恒星月、もう一つは太陽を基準とした周期(満ち欠けの周期)である朔望月である。
1恒星月:地球から見て、月がある恒星の向きに見えてから再び同じ恒星の向きに見えるまで=27.32日。
1朔望月:満ち欠けの周期。新月(満月)から新月(満月)まで=29.53日。
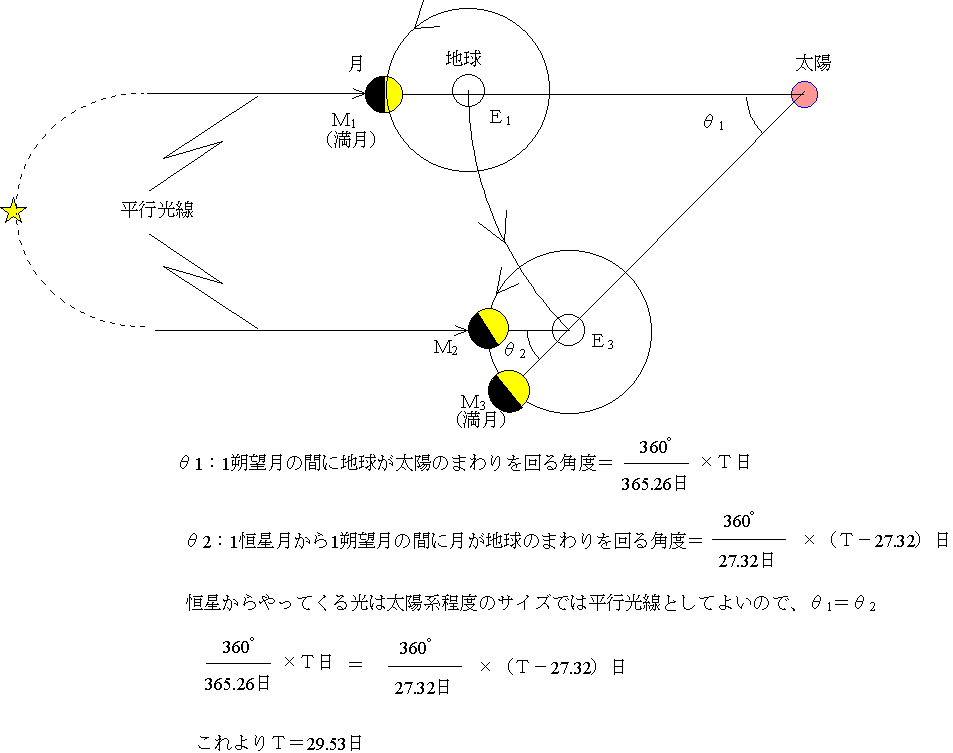
ここで、恒星月(27.32日)から朔望月(29.53日)を導いてみよう。あるときの地球(E1)から見て、月(M1)が満月になった。そのとき、月は地球から見てある恒星の向きに見えた。月は地球のまわりを矢印の方向に回っているが、その間にも地球は太陽のまわりを矢印の向きに回っている。そこで、次にこの月がある恒星の向きに見えるのは(1恒星月後)M2のときである。しかしこの位置ではまだ満月ではない。満月になるにためは(1朔望月後)、あともう地球は少し太陽のまわりを回らなくてはならない。そこで1朔望月をT日とすると、下の図・計算のようにして、T日を求めることができる。なお、こうしたときは基準を揃えなくてはならないので、地球の公転周期も月の公転周期(1恒星月)と同じく、恒星を基準とした1恒星年の数値にしている。
大きな視点で月の運動を見るとどうなるだろう。地球は太陽のまわりを回っていて、その地球のまわりを月が回っている。つまり、太陽(宇宙)からみると、月の速さは動いている地球の速さに乗った速さになる。例えば下の図のように太陽(宇宙)から見た月の速さは、月と地球の公転の速さをそれぞれVM、VEとすると、満月のときはVE+VM、新月のときはVE−VMになる。
地球と月の距離、地球と太陽の距離は、地球の半径をRとすると、それぞれ60R、24000Rであり、地球や月の公転軌道はほぼ円なので、それぞれの公転軌道の長さは月が2π・60R、地球が2π・24000Rとなる。この公転軌道の長さを、月と地球の公転周期TM、TEで割れば、それぞれの公転の速さVMとVEがわかる。
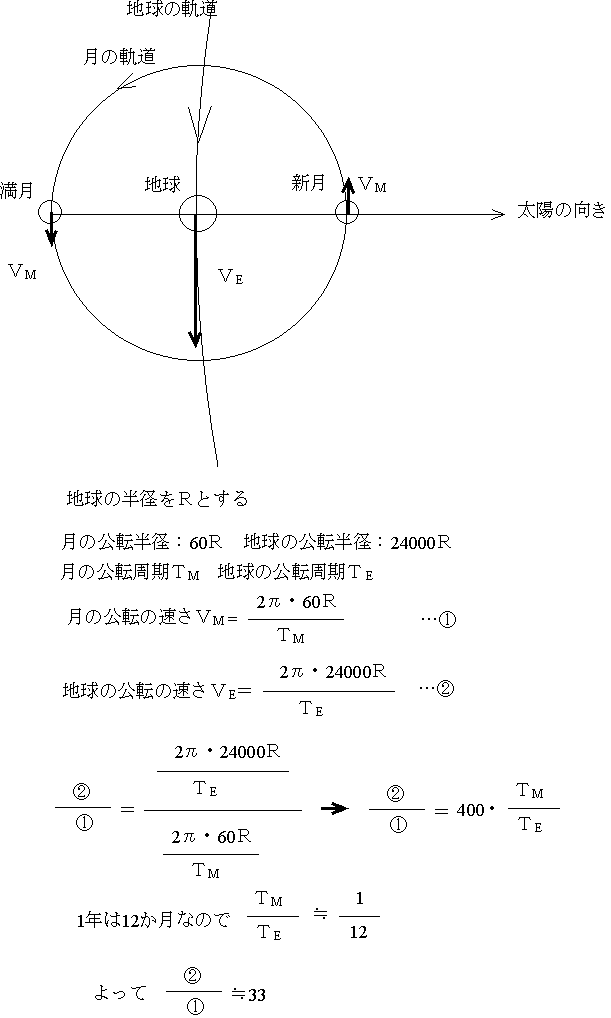
これからわかるように、地球の公転の速さの方が月の公転の速さの30倍以上も速いことがわかる。つまり、動いている電車に乗っている人が、その電車の中で電車の進行方向と逆向きに走っても、電車の外からその人を見てみると電車の動いている向きに動いているように見えるのと同じで、太陽(宇宙)から月の動きを見ると、月はつねに地球の進行方向と同じ向きに動いているようにしか見えないのである。このことは、月はループを描くようには見えず、地球の軌道を微妙に横切りながら地球とともに太陽のまわりを回っていることを意味している。
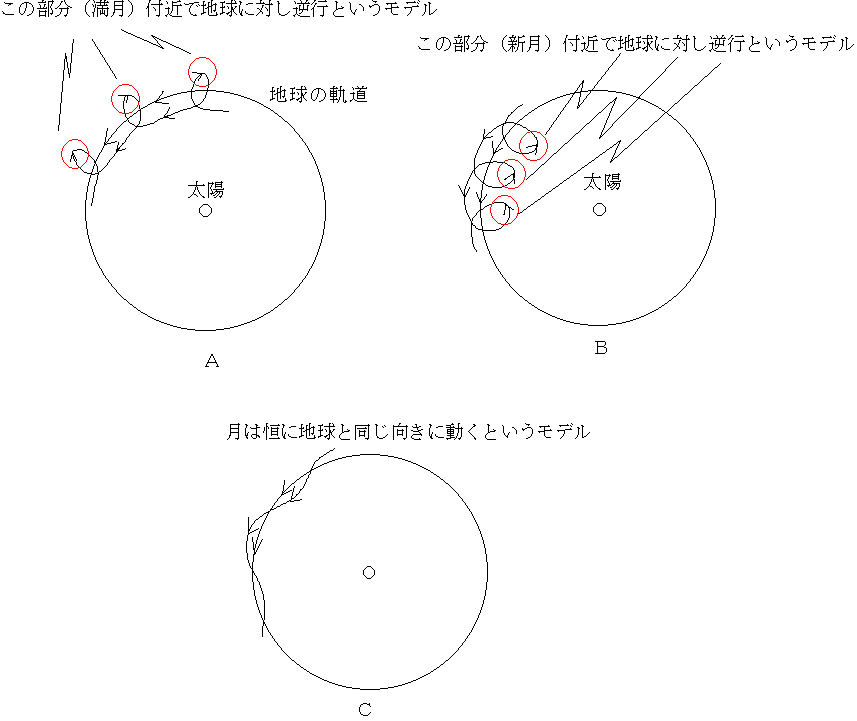
つまり、下の3つのモデルのうち、Aのような満月付近で地球の動きに対し逆に動くということは(ループを描くということは)、上の図のように満月付近ではそもそも月の動く向きは地球の公転の向きと同じなので、あり得ないということがすぐにわかる。あと、Bの新月付近で地球に対して逆に動くかどうかということも(ループを描くかどうかということも)、上の計算結果から地球の公転の速さの方が圧倒的に速いので、これまたあり得ないことがわかる。だから、太陽(宇宙)から見た月の動きは、つねに地球の公転の向きと同じになっているCのような動きということになる。
月の見かけの形:現在の文部科学省の学習指導要領では、小学校4年生の理科で月の見かけの形の変化を扱うが、なぜそのような見かけの形が変化するかまでは追求しない。それどころか、月の見かけの形も「三日月や満月などの中から二つの月の形を扱うこと」明記されている。つまり二つの形しか扱わない。
また、中学校の理科(第2分野)においては、「惑星の見え方については,内惑星のみを扱うこと」とあるので、金星の見かけの形の変化(望遠鏡を使わないとわからない)は扱うが、月の見かけの形の変化は扱わない。
つまり、非常に身近な現象である月の満ち欠けに関して、その原因やいろいろな形とその呼び名については、義務教育段階ではまったく習わないようになっている。
望月:満月のことを望(ぼう)、あるいは望月(もちづき)という。望月は名字にも用いられている。平安時代の権力者・藤原道長(966年〜1027年)は、1018年に自分の娘の威子が後一条天皇の后になったお祝いの席で(すでに他の娘二人も天皇家に嫁いでいる)、「此の世をば 我が世とぞ思ふ 望月の 欠けるたる事も 無しと思へば」(この世のすべては思いのまま、満月が欠けることさえなければ)とその得意の気持ちを謳っている。
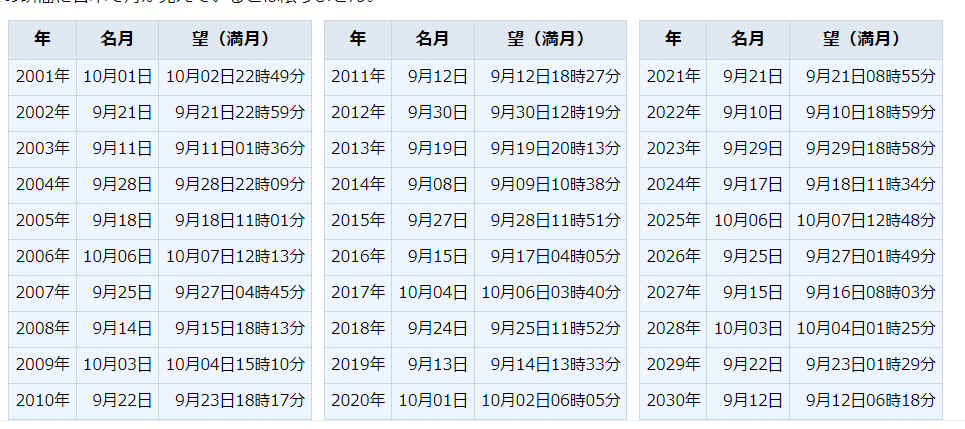
中秋の明月:じつは旧暦で15日が必ず満月というわけではない。厳密には、旧暦十五日の正午の月齢が14なので、実際の満月はそれより1日後になることが多い。2001年から2030年までの中秋と満月は以下の通り。
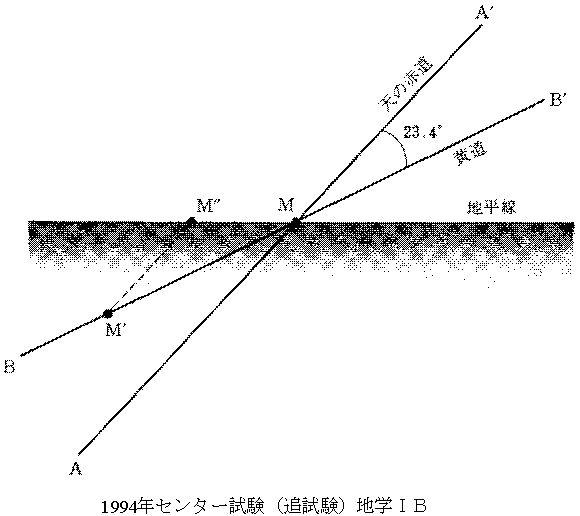
ここで、話を簡単にするために、秋分の日に満月になったとする。すると月は天球上では太陽(秋分点にいる)の反対側の春分点にいる。下の図は、この満月が地平線上のMの位置から昇ってくるときの東の空を、北半球の中緯度地方で見たもので、AA’は天の赤道、BB’は黄道である。図のように天の赤道と黄道がなす角度は23.4°である。天球上で月が黄道上を動くとすると(白道と黄道が一致しているとすると)、翌日の同じ時刻に月はM’の位置にあり(月は天球上の西から東へ(図では左から右へ)動くので)、月は約30日で天球上を一周する(360°回る)ので、MとM'が天球上でなす角度(角距離)は約12°である。月はAA'と平行にMM″と昇ってくる。このMM″に要する時間が翌日の月の出の時刻の遅れとなる。このとき、黄道と地平線のなす角度は1年のうちで最小になるので、1日ごとの月の出の遅れも1年を通じて最小になる。だから、このころの東の空の満月を愛でるのは、東の空に長く明るく輝いているので、非常に都合がいいことになる。
月の公転周期と距離:月(の引力、厳密には潮汐力)は地球の自転にブレーキをかけている。そのかわりに月は地球から遠ざかっている(角運動量の保存)。そして、地球もいつも同じ面を月に向けているようになると、その状態で安定すると考えられる。そのときの地球の自転と月の公転周期(=自転周期)は60日程度と考えられている。こうなったときの月までの距離をケプラーの第3法則を使って計算すると約65万km(現在の距離の約1.8倍の距離)となる。1年で約4cmずつ遠ざかっているとして、68億年後ということになる。実際は遠ざかるほど潮汐力は弱くなる(距離の3乗に反比例)ので、もっと時間はかかる。
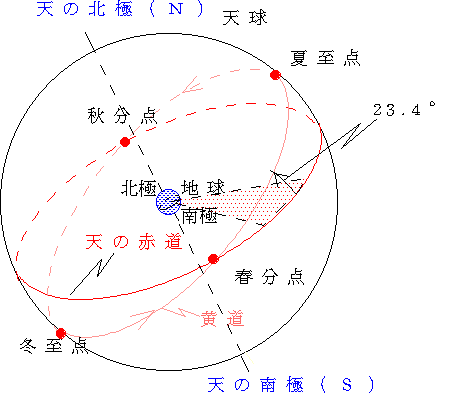
月の軌道(1):天球上の月の軌道を白道(はくどう)という。白道(月の公転面)は黄道(天球上の太陽の通り道=地球の公転面)に対して、約5.9°傾いている。だから、新月のたびに日食(太陽−月−地球が一直線上に並ぶ)、満月のたびに月食(太陽−地球−月が一直線上に並ぶ)ということにはならない。
冬の満月は南中高度が高いという。白道と黄道がほぼ一致していると考えれば、冬の満月は天球上では冬至点近くにある太陽の反対側の夏至点付近にあることになる。だから冬の満月の南中高度は北緯35°の地点で78.4°±5.9°となり、たしかに高度は高いことがわかる。
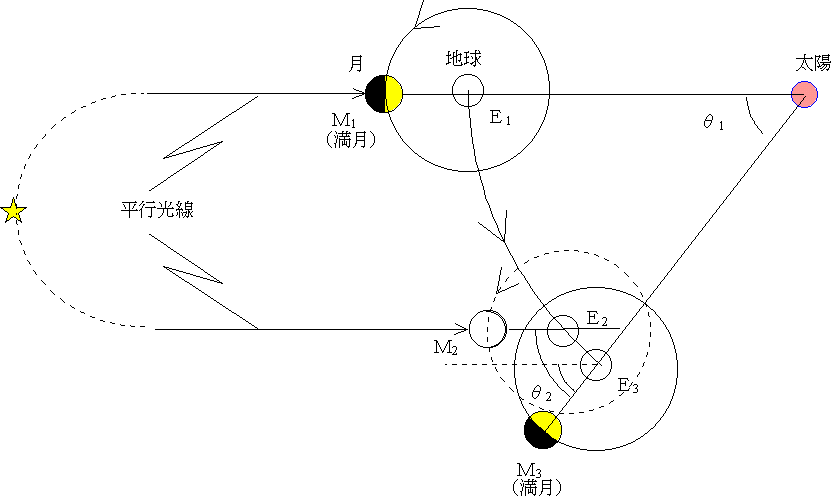
朔望月:1恒星月から朔望月になるまでにも、地球は太陽のまわりをE2の位置からE3の位置まで回っている。そこでもう少し厳密な図を描くと下のようになる。しかし、計算そのものは上で行ったとおりでよいことがわかる。
月の軌道(2):厳密にいうと、C図も正しくはない。地球や月の公転を支配しているのは万有引力である。万有引力は、質量の積に比例して、距離の二乗に反比例する力である。ここで、太陽が月に及ぼしている引力(同じ力で月は太陽に引力を及ぼしている)と、地球が月に及ぼしている引力(同じ力で月は地球人力を及ぼしている)を比べてみる。地球の質量をMとすると、太陽の質量は3.3×105M、月の質量は1.2×10-2M。地球の半径をRとすると、地球−太陽間(月−太陽間としてよい)の距離は2.4×104R、地球−月間の距離は6.0×10R。万有引力定数はGとする。
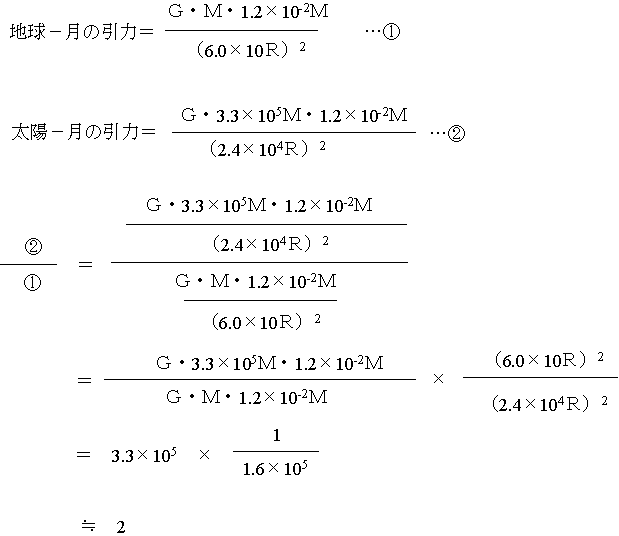
このように月に及ぼしている力を比べると、太陽の方が地球よりも2倍も大きいことがわかる。だから、たしかに地球−月だけを考えれば月は地球のまわりを回っているといってもいいが、太陽−地球−月を考えると、地球も月も太陽のまわりを回っている、そして月の軌道は地球の引力のために少しぶれて1年に12回ほど地球の軌道を横切るということになる。月も太陽のまわりを回っているということは、月の軌道はC図のように太陽に対して凸になることはなく、つねに凹になっているということである。少し作図はしにくいが、下図のような微妙な感じになる。これについてはこちらも参照。

月探査情報ステーション:http://moon.jaxa.jp/ja/index_fl.shtml