| このページの目次 | ||
| 第2章 月(1) | ||
| 1.月までの距離と大きさ・質量 | ||
| (1) 月までの距離 | ||
| a.三角測量 | ||
| b.光や電波の反射を利用する | ||
| c.ケプラーの第三法則を使う | ||
| (2) 月の直径(半径) | ||
| (3) 月の質量 | ||
| 用語と補足説明 | ||
| 参考になるサイト | ||
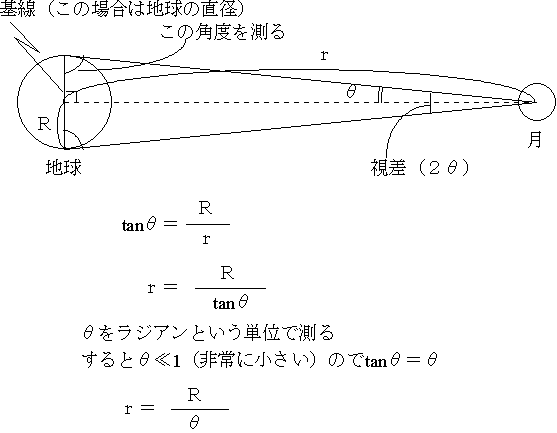
長さがきちんとわかっている線(基線という)の両端から距離を測りたいものを見込んで、基線とそのものがなす角度を測ると視差(下図参照がわかる。基線の長さを一定とすれば、近いものほど視差が大きく、遠いものほど視差が小さい。また距離が一定のときは、基線が短いと視差が小さく、基線が長いと視差が大きくなる。だから、遠いものまでの距離を測るときは、基線の長さを長くした方が正確な視差を測定できるので、正確な距離を測定できることになる。
三角測量については、恒星までの距離、地球の公転の証拠の一つ年周視差の項も参照。
地球上でとることができる一番長い基線は地球の直径である。だから、この両端から月を見込んで視差を求めれば、月までの距離が測定できる(実際にはもっと短い基線でもよい)。地球の半径R、このときの視差の大きさを2θ(シータ)とすると、月までの距離は下のようにして求めることができる。ここで、角度の単位として弧度法(ラジアン)を使うと、θの値が非常に小さいときはtanθ=θという関係があるので、直接月までの距離を求めることができる。なお、弧度法(ラジアン)や三角比(三角関数)はそれぞれを参照。

θは1.66×10-2radなので、地球の半径をR(6.37×103km)とすると、r=(6.37×103km÷1.66×10-2)=3.84×105km(384000km)となる。もう少し正確には、384400kmである。ただし、月の軌道は完全は円ではなくだ円なので、地球と月の距離は少し変化する。だから、この値は平均値である。月までの距離は、地球の半径の約60倍である。なお、太陽までの距離は地球の半径の約23500倍(約24000倍)である。
月にレーダーの電波をあてて、その電波が戻ってくる時間を測定することによっても、距離を求めることができる。じっさいには、月面には月に着陸したアポロ宇宙船(11号、14号、15号)が設置した鏡(光がどの向きから入ってきても、その向きに反射する鏡)があるので、そこにレーザ光線を当てて、その反射にかかった時間で距離を求めている。こうすると、非常に正確に月までの距離を求めることができる。こうして月までの距離を測ってみたところ、月は毎年地球から約3.8cmずつ遠ざかっていることがわかった(「太古、月は近かった」大江政嗣、「生きている地球の新しい見方」(グアプロ、平成11年10月)の中の一編)。

月面に置かれたレーザ光線反射鏡
http://nssdc.gsfc.nasa.gov/image/spacecraft/apollo_laser_reflector.jpg
月の公転周期から、ケプラーの第3法則を使うと、地球と月の距離(お互いの重心間の距離)を求めることができる。昔はこの方法が主だった。
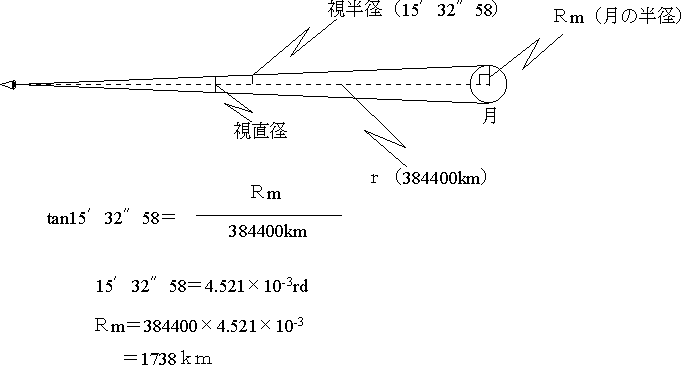
(2) 月の直径(半径)
距離がわかれば、あとはみかけの大きさ(視直径、視半径)を測定すれば、直径(半径)がわかる。月の視半径は平均で15′32″58である。これをラジアン(rad)に直す。1′が60″であることに注意して、15′32″58=932.32″。360°=2πradだから、1″=4.848×10-6rad。これより15′32″58=4.521×10-3rad。つまり、tan(15′32″58)=tan(4.521×10-3rad)=4.521×10-3rad。これより、月の半径が1738kmであることが求められる。この大きさは地球の約1/4である。
この月の大きさは太陽系の衛星(惑星のまわりを回る天体)の中で5番目に大きく、衛星:母惑星(月に対する地球など)の比としては大変に大きい。例えば、太陽系最大の衛星は木星(半径71492km)の衛星ガニメデ(半径2634km)であるが、その大きさは木星の約1/30でしかない。これらについては、惑星・衛星の一覧表を参照。
地球を半径1cmの球(1円玉の大きさ)とすると、月はそこから60cm離れたところにある半径0.25cm(直径5mm)の球となる。このとき、太陽は約240m離れたところにある半径110cm(半径1.1m)の球となる。
(3) 月の質量
月の質量は、地球のまわりを回る月の公転周期からケプラーの第3法則を使って求めることができる。最近では、月のまわりを回る人工衛星の飛び方からもっと正確に月全体の質量や、さらに月の場所による密度の違いまでを測定することができる。
こうして求めた月の質量は、地球の質量の0.0123倍(1.23×10-2倍)という憶えやすい値である。なお、地球の質量は5.98×1024kgである。この月の質量と、月の半径から求めた月の体積(半径rの球の体積は4πr3/3)から、月全体の平均密度を求めることができる。
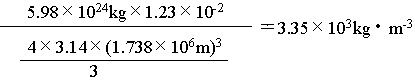
この月の密度(3.35×103kg・m-3)は、花こう岩(2.7×103kg・m-3)、玄武岩(2.8〜3.0×103kg・m-3)、かんらん岩(3.3〜3.4×103kg・m-3)、隕石(石質隕石、3.6〜3.8×103kg・m-3)程度といえる。つまりこの密度は、鉄(7.8×103kg・m-3)などの金属よりははるかに小さい。
このことは、月はほとんど岩石でできていて、地球のような金属の核(外核・内核)はないか、あっても小さいということを意味している。
レーザ光線反射鏡:コーナーキューブ・ミラーという鏡を使うと、その鏡で反射した光はもとの向きに反射される。この鏡は互いに直角な3枚の鏡からできている。だから、立方体の3面を下の図のように利用すればよい。
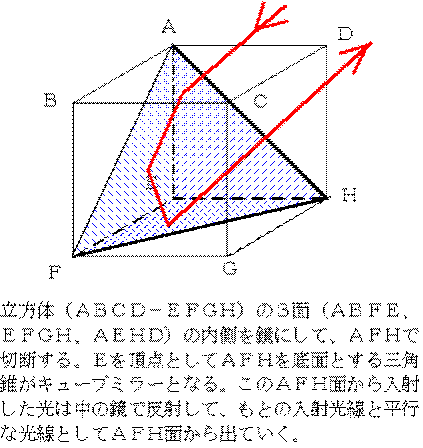
いきなり立体(3次元)では考えにくければ、平面(2次元)で考えるとわかりやすい。下の図のように2枚の鏡を直角に置けば、この鏡に反射する光は、入射してきた向きと平行になって出ていくことがわかる。
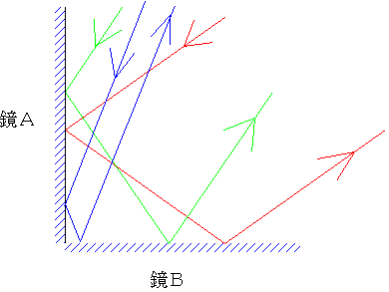
こうした鏡は別に特殊なものではなく、自転車の後ろについている反射鏡、道路の脇のガードレールなどについている反射鏡もこうしたコーナーキューブ・ミラーである。車のライトの光がこうした鏡に当たればもとに戻るので、必ず車の運転手の目に入るわけである。
月探査情報ステーション:http://moon.jaxa.jp/ja/index_fl.shtml