トリチェリーの実験:国土環境株式会社
http://www.bioweather.net/column/weather/contents/mame046.htm
第3章 大気圧
1.大気圧
空気も“もの”である以上質量がある。そして地球上では質量があれば地球の重力によって引きつけられている。つまり大気も重力によって引きつけられ、地表を押す力(重さ)となる。これが大気圧である。厳密にいうと、圧力とは一定の面積(1m2)に加わる力であるので、大気圧も1m2に加わる大気の重さによる力ということになる。
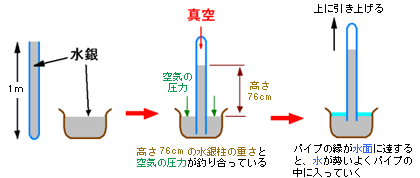
この大気圧を目に見える形で示したのが、一時ガリレオ(イタリア、1564年〜1642年)の秘書もやったことがあるトリチェリー(イタリア、1608年〜1647年)であった。彼は、下のように長さ1mくらいのガラス管に水銀を満たしてからふたをして、同じく水銀を満たしたお皿にそのガラス管を逆さにしてたててた後、ガラス管のふたをはずすと、ガラス管の中の水銀はすっと下がり、お皿の水銀面からの高さ約76cmで止まることを示した(1644年)。つまりこれはお皿の水銀面を押す大気圧(空気の重さ)と、ガラス管の中の水銀柱の重さが釣り合っていることを示す。だから、それ以上は水銀柱は下がってこないのである。また、水銀柱の上には何も入り込めないので真空になっているはずである。この部分をトリチェリーの真空という。
さらにお皿の水銀の上に水を加え、その水の所までガラス管を引き上げると、水は水銀柱の中に吸い込まれて上に登っていくことも示している。

トリチェリーの実験:国土環境株式会社
http://www.bioweather.net/column/weather/contents/mame046.htm
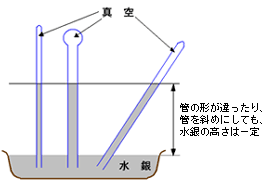
さらにパスカル(フランス、1623年〜1662年)は、ガラス管のの太さや形を変えても、あるいはガラス管を傾けても、ガラス管の中の水銀柱の高さは一定になることも示した。これは一見不思議なことだが、逆に釣り合っているのは一定の面積に加わる圧力であるということがわかる。これをパスカルの原理という。
パスカルの実験:国土環境株式会社
http://weather.metocean.co.jp/column/otenki17.htm
こうして、トリチェリーやパスカルはわれわれ人間は大気(という海)の底に住んでいるという考えを持つに至った。さらにパスカルは、もし人間が大気の底に住んでいるのならば、深い水中よりも浅い水中画の圧力(水圧)の方が小さいことと同じように、高いところに登れば大気圧は小さくなるはずであると考えた。彼は体が弱いので、このことを姉の夫ペリエに頼ん、高い山に登ると水銀柱の高さが76cmまで登らないことを確かめてもらった。
この実験は水銀の代わりに水を使ってもできるはずであるが、実際にはいろいろな制約があって水では正しく大気の圧力を測ることができない。
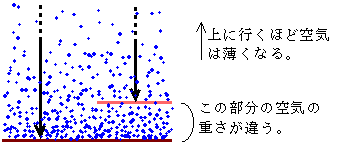
下の図で地表では上から下までの空気の重さを受けるが、高いところ(赤い線の高さ)では、それ以上の高さに存在している空気の重さしかかからないのである。逆にいえば、地表から赤い線までに存在している空気の重さの分だけのしかかってこないわけであり、その分だけ気圧は小さくなる。つまり、大気圧とはその上に存在している空気の重さと考えればよい。
なお、下の図のように空気は圧力をかけると縮んでくる。だから逆に上空ほど薄く(密度が小さく)なっている。高さによる空気の密度の変化のグラフはこちらを参照。
2.大気圧の大きさ
平均的な大気圧は76cm(0.76m)の水銀柱による圧力に相当する。水銀の密度は0℃のときに13.5951×103kg・m-3である。だから、高さ0.76mの水銀柱の質量は、断面積を1m2とすれば13.5951×103kg・m-3×0.76m3=1.03323×104kgとなる。この質量は地球の重力により、重力加速度9.80665m・s-2(標準の値、1901年国際度量衡総会で定義された)をかけた1.01325×105Nという力、つまり1m2あたり1.01325×105Nという圧力、すなわち1.01325×105Paという圧力となる。
普段は感じることはないが、これは大変な圧力である。1m2あたりで10tonに相当する重さ(小型乗用車6〜7台分)がかかっていることになる。1cm2あたりにしても約1kgということになる。
この1.01325×105Paが標準大気圧といわれるもので、これが1気圧(1atmと書く)となる。これは上に示したように76cmの水銀柱による圧力に相当する。古くは水銀柱の高さをミリメートルで測り、それそのもので気圧を表していた。今でも血圧だけはその風習が残っている。血圧が100とは、100mmHg(100水銀柱ミリメートル)のことである。
実際には気象関係で用いられる気圧は、100倍を表す接頭語h(ヘクト)を用いて、hPa(ヘクトパスカル)という単位で表す。これは、かつて圧力をbar(バール)という単位で表していた時代、気圧はその1000分の1のm(ミリ)を用いて、mb(ミリバール)という単位を使っていたときに、1atm=1013mbという数値になっていた。そこで、その数値をあわせるために少し変則であるがh(ヘクト)を使うと、1atm=1013hPaとなり数値だけを取り出せば同じなる。これは、これまでに蓄積した過去のデータを利用するときに大変に便利である。
地表(海抜0m)で1013hPa、気温288.15K(ケルビン)(15℃)のときに、高さとともに気圧や空気の密度がどう変わるかは下を参照。おおざっぱにいうと、高さ3000m(3km)程度までは、高さ100mごとに気圧は10hPaずつ下がっていることがわかる。これを逆に使うと、気圧を測ることによって高さ(高度)がわかることになる。簡便な高度計(時計などに組み込まれているもの)は、圧力センサーを内蔵しているので気圧を測定することができ、その気圧によって高さを求めるものである。気圧そのものは変動するので、高さがわかっている場所で補正することによってより正しい高度を出すことができる。
さらに、高さ5000m(5km)での気圧は、地表の気圧の約1/2になっている。高さ20kmでの気圧は地表の約1/20になっているが、これはそれ以上の高さの大気は全体の1/20しかないことを示している。逆にいうと、高さ20kmまでの大気で、大気全体の19/20(95%)になることがわかる。
水の沸点は1atmで100℃(厳密には99.974℃)であるが、700hPa(高さ3000mくらい)で約90℃、470hPa(高さ6000m)で約80℃になってしまう。
3.海面更正
高さが異なる観測点で測った気圧をそのまま比較しても意味はない。例えば気象庁の観測所がある長野は標高418.2m、松本は610m、軽井沢にいたっては標高999mまある。標準的な状態では、海抜0mで1013hPaでも、長野は960hPaくらい、松本は940hPaくらい、軽井沢は900hPaくらいになっている。これをそのまま比べると、これらの場所ではいつも低気圧ということになる。そこで、気圧を比較するときには必ず海抜0mの値に換算する。これを海面更正という。天気図を書くときの基本データとなる各地の気圧はこのように海面更正された後の値が発表される。
4.大気の総量
地表の1m2あたりに1.03323×104kgの質量の大気が存在しているということは、この値に地球の表面積(510×1014m2)をかければ、地球の大気の総量が求まることになる。つまり地球は5.25×1018kgの大気を持っていることになる。海水の総量は1.42×1021kgであるので、大気はその約1/270ということになる。
別な考え方をすると、水は10mの深さでで約1atm(正確には10.336mで1atm)、海の平均の深さは3800m、ただし、海は地球表面の70%なので全地球表面で平均すると2700mとなる。圧力では270atm。つまり海水は地球大気の270倍の質量ということになる。
なお、もし地球が金星のような状態になったら、海水は全部蒸発して水蒸気による気圧が270atm、さらに石灰岩が熱で分解して発生する二酸化炭素による圧力が30atm〜50atmと想像されているので、全部で300atm〜320atmという金星よりも濃い大気となることがわかる。これについてはこちらも参照。
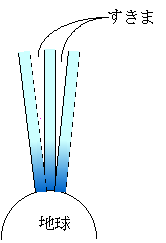
なお、上のように計算した大気の総量は、大気の柱をそのまま上にのばして、その中に含まれる大気の量を計算したことになる。だから、厳密に考えると下図のすきまに存在している大気を無視していることになる。しかし、実際には地球の半径6400kmに対して、わずか20km(半径の1/320)の高さの範囲内に全大気の95%が含まれているわけだから、このすきまが目立ような幅の高さになると、そこに存在している空気はごくわずかで無視できることがわかる。
トリチェリーの真空:それまでは古代ギリシャの偉大な哲学者アリストテレス(紀元前384年〜紀元前322年)の考え、すなわち「自然は真空を嫌う」という考えが一般的で、真空ということはあり得ないと思われていた。トリチェリーの実験によって、真空が存在することが確かめられた。すでにガリレオは通常のポンプでは井戸水は10m以上の深さからは汲み上げられないことを発見していた。つまり、「自然は真空を嫌う」から水がポンプ(やストロー)で吸い上げられるのではなく、大気圧で押し上げられるので、吸い上げられるということがわかったのである。
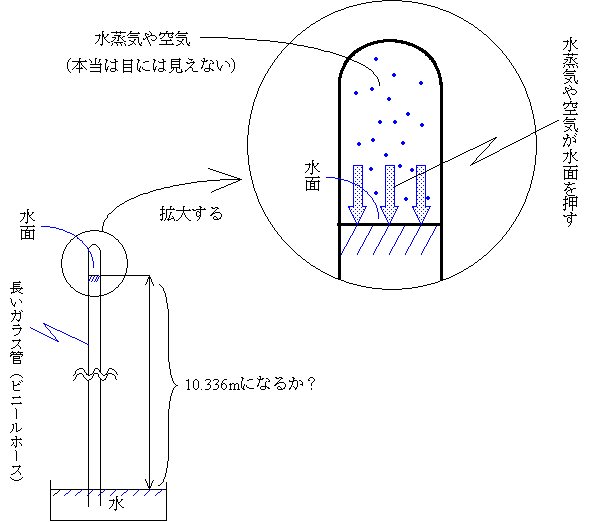
水を使ったトリチェリーの実験:水は水銀の密度の約1/13.6であるので、水を使うと水柱の高さは76cm×13.6=1033.6cm(10.336m)の高さになるはずである。だから、それだけの長さのガラス管、もちろん透明なビニールホースがあれば実験できることになる。
しかし実際には水柱の高さはそのような高さにはならない。これは、下図のようにガラス管(ビニールホース)内の水面から、水が蒸発して水蒸気になること(この部分気圧が低いので水は蒸発しやすい)、またふつうの水には空気が溶け込んでいてその空気がこの部分に出てきてしまうこと、この水蒸気や空気がガラス管(ビニールホース)内の水面を押すので、10.336mの高さにはならないのである。つまり、トリチェリーの実験のように真空はできないのである。
パスカル:ブレーズ・パスカル(Blaise Pascal、フランス、1623年〜1662年)は、数学者・科学者・宗教家である。パスカルの伝記は3歳年上の姉ジルベルトが書いている。この伝記は日本語に訳されているのでそれを読むことができる。この姉ジルベルト、そしてパスカルには妹もいたが、二人ともパスカルを溺愛しており、この伝記でも「うちの弟は小さいころからこんなにすごかった。」ということを書き連ねている。だが、パスカルを溺愛した肉親が書いたものであるからこそどこまで本当かはにわかには信じがたい(宗教的な問題もあり、弟はこんなに篤信家で会ったことも書き連ねている)。例えば、父からは数学の勉強を禁止されていたが、少年パスカル(12歳ころ)は独力でユークリッド幾何学を構築(三角形の内角の和が二直角であるという定理=第1巻定理32までを順に発見)しつつあったという。

パスカル:http://www-groups.dcs.st-and.ac.uk/~history/PictDisplay/Pascal.html
しかし、16歳のときに「円錐曲線論」を書いたのは確かである。数学面ではのちに(35歳のときに)、サイクロイドという曲線の研究もしている。姉ジルベルトにいわせれば、これも歯痛を忘れるために一晩で考えたという。ほかにも、友人のフェルマとともに確率論を始めたりもしている。パスカルの三角形はこれと関係している。
科学者としてのパスカルは、伝え聞いたトリチェリーの実験を追試して正しい大気圧(逆にいえば真空)の概念を得るに至った。また、流体に関するパスカルの原理も発見している。
また、一時引退してパスカルの養育に専心していた父(母はパスカルが3歳の時に死亡)が税務署長として赴任したため、その父の仕事を助けるために苦労に苦労を重ねて計算器も発明・作成した(パスカル18歳のころ)。この苦労のために、もともと体が弱かったパスカルはさらに体を弱くしたという。もっともこれも姉にいわせると、パスカル自身は簡単に計算器の原理を考え出したが、それを職人に理解させることに苦労したという(製品化するまでに2年かかった)。パスカルはこれで商売を行うつもりであったらしいが、どの程度儲かったのだろう。このパスカルの計算器は加減が行えるだけであったが、ライプニッツ(ドイツ、1646年〜1716年)はこれを改良して乗除や開平(平方根を開くこと)も行えるようにした。なお、加減乗除を行える近代的な機械式計算器(手回し計算器)の写真はこちら。
 |
 |
| パスカルの計算器とその中の様子:http://www.ulisse.bs.it/museo/storia/pascal/pascal.htm | |
宗教家(思索者)としてはパンセ(随想録)の著者として有名である。「人間は考える葦である。」は彼のこうした面を代表する言葉である。彼は24歳のとき、氷ですべって足を脱臼した父の治療にあたった医者を通じて、フランスの宗教改革運動ジャンセニスムを知る。ジャンセニスムは有名な男子修道院団体イエズス会と厳しく対立していた。ジャンセニスムに共感するパスカルは否応なく宗教界の対立に巻き込まれていく。こうしたことも、彼の体をむしばんだのだろう。
病弱な彼は医師の薦めで(!)社交界に出入りするようになる。そこでもファンを獲得したらしいが、すでに修道院入りしていた(兄の影響で修道院入り?)妹の薦めもあり、さらに乗っていた馬車の暴走事故を起こしたときに奇跡的に助かったこともあり、33歳の彼は完全に社交界から足を洗って隠遁生活に入ってしまう(パスカルの大回心)。とはいえ、サイクロイドの研究は35歳のころだし、病苦(おもに頭痛)と闘いながら死ぬまでジャンセニスムの拠点ポール・ロワイヤル修道院のために働いていたのである。
死ぬときは姉の家で、姉に看取られながら死んでいった。最後の言葉は「神が私を見捨てぬように」だったという。思うに、ケプラーにしろパスカルにしろ、偉大な科学者、あるいは科学者でなくとも坂本龍馬みたいな人には優しい姉(パスカルには妹も)がいる。優しい姉がいることが偉大な人になれる必要条件かもしれない。もちろん、優しい姉がいれば偉大な人になれるというわけではない。つまり、十分条件ではない。
サイクロイド:平面の上に垂直に立った円の円周の一点が、円が回転することによって描く図形。高さの違う2点P、Q(Pのほうが高いところにある)があるとき、重力だけで落下するときに最も速くPからQに到達するのはこのサイクロイドという曲線であるので、最速降下曲線ともいわれる。ニュートンの項も参照。このサイクロイドという形は高精度の歯車に利用されている。
サイクロイドについては小島淳子氏の下記のサイトで見ることができる。
http://www.junko-k.com/jyoho/simulation/flash-cycloid.htm
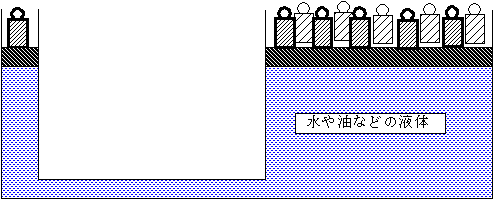
パスカルの原理:閉じこめられた流体の一部に圧力を加えると、その圧力は流体のすべてに伝わる。これをパスカルの原理という。例えば、断面積の異なる二つのシリンダーに液体を入れて、それらをパイプで結びんで見る。すると、下図の左のシリンダーでは一つのおもりが、右の断面積が10倍であるシリンダーでは10個のおもりと釣り合っている。でも、一定の面積にかかる力は同じなので釣り合うのである。これはてこと同じで、小さな力を加えても、明治産業株式会社の「現在のブレーキ」参照。また、てこと同じように小さな力で大きな力を得るといっても、エネルギーで得をしているわけではない。下の図で、左のシリンダーを例えば10cm押し下げてやっと右のシリンダーが1cm上がることになる。
トリチェリーの実験で、ガラス管の太さや形に関係なく水銀柱の高さが一定になるのは、釣り合っているのが一定の面積に加わる力、すなわち圧力であるからである。
こうして圧力の概念をはっきりとさせたパスカルを記念して、圧力の単位はPa(パスカル)となった。1Paは1m2に1N(ニュートン)の力が加わっていることになる。1Nという力についてはこちらを参照。
フェルマ:ピエール・フェルマ(Pierre de Fermat、1601年〜1665年)。職業は法律家。趣味で数学や物理の研究を行っていた。プロの賭博師から、賭を途中でやめたときの掛け金の分配を相談されたことをきっかけに、友人パスカルと確率論の研究を始めた。また、光の研究も行い、光が屈折・反射して別な場所に届くときは最小の時間になるような経路を通るという光学におけるフェルマの原理も打ち出している。波の屈折の法則(スネルの法則)は、このフェルマの原理から導くことができる。
フェルマが有名なのは、数学における「フェルマの最終定理」をいい出したからであろう。彼は自分の研究を読んでいる本の余白に書くのがつねであった。これも、「私は nが3以上のとき、an+bn=cnを満たす整数a、b、cがないことを発見し、証明もしたが、その証明はこの余白では狭すぎる。」と書き記した。フェルマが本当に証明できたかどうかは謎であるが(たぶん間違っていただろう)、完全な証明は1994年にアメリカのプリンストン大学の数学者アンドルー・ワイルズによってなされた。
なお、nが2のときは、a2+b2=c2というピタゴラスの定理となり、これを満たす整数a、b、cは無数に存在している。
イエズス会:カトリック会の中の男子修道院組織。16世紀初めころにフランスで創設される。活発な宣教師派遣活動を行っていて、その一人フランシスコ・ザビエルは日本に最初にキリスト教を伝えることになる。一時ローマ法王によって閉鎖されるが(1773年〜1814年)、のちに復権して今日まで続いている。1614年の江戸幕府のキリシタン禁止令で一時日本から手を引いたが、1908年に再渡来して上智大学の創設などの教育活動並びに布教活動を行っている。
高さと気温・気温・密度:標準的な状態での、高さと気温・気圧・密度は下の表のようになっている。理科年表2004CD-ROM版(丸善)による。
| 高度 | 気温 | 気圧 | 密度 |
| Z(km) | T(K) | P(hPa) | ρ(kg/m^3) |
| 0 | 288.15 | 1.01325×10^3 | 1.225 |
| 1 | 281.651 | 8.9876×10^2 | 1.1117 |
| 2 | 275.154 | 7.9501×10^2 | 1.0066 |
| 3 | 268.659 | 7.0121×10^2 | 9.0925×10^{-1} |
| 4 | 262.166 | 6.1660×10^2 | 8.1935×10^{-1} |
| 5 | 255.676 | 5.4048×10^2 | 7.3643×10^{-1} |
| 6 | 249.187 | 4.7217×10^2 | 6.6011×10^{-1} |
| 7 | 242.7 | 4.1105×10^2 | 5.9002×10^{-1} |
| 8 | 236.215 | 3.5651×10^2 | 5.2579×10^{-1} |
| 9 | 229.733 | 3.0800×10^2 | 4.6706×10^{-1} |
| 10 | 223.252 | 2.6499×10^2 | 4.1351×10^{-1} |
| 11 | 216.774 | 2.2699×10^2 | 3.6480×10^{-1} |
| 11.1 | 216.65 | 2.2346×10^2 | 3.5932×10^{-1} |
| 12 | 216.65 | 1.9399×10^2 | 3.1194×10^{-1} |
| 13 | 216.65 | 1.6579×10^2 | 2.6660×10^{-1} |
| 14 | 216.65 | 1.4170×10^2 | 2.2786×10^{-1} |
| 15 | 216.65 | 1.2111×10^2 | 1.9476×10^{-1} |
| 16 | 216.65 | 1.0352×10^2 | 1.6647×10^{-1} |
| 17 | 216.65 | 8.8497×10 | 1.4230×10^{-1} |
| 18 | 216.65 | 7.5652×10 | 1.2165×10^{-1} |
| 19 | 216.65 | 6.4674×10 | 1.0400×10^{-1} |
| 20 | 216.65 | 5.5293×10 | 8.8910×10^{-2} |
| 21 | 217.581 | 4.7289×10 | 7.5715×10^{-2} |
| 22 | 218.574 | 4.0475×10 | 6.4510×10^{-2} |
| 23 | 219.567 | 3.4668×10 | 5.5006×10^{-2} |
| 24 | 220.56 | 2.9717×10 | 4.6938×10^{-2} |
| 25 | 221.552 | 2.5492×10 | 4.0084×10^{-2} |
| 26 | 222.544 | 2.1883×10 | 3.4257×10^{-2} |
| 27 | 223.536 | 1.8799×10 | 2.9298×10^{-2} |
| 28 | 224.527 | 1.6161×10 | 2.5076×10^{-2} |
| 29 | 225.518 | 1.3904×10 | 2.1478×10^{-2} |
| 30 | 226.509 | 1.1970×10 | 1.8410×10^{-2} |
| 32.2 | 228.756 | 8.6314 | 1.3145×10^{-2} |
| 35 | 236.513 | 5.7459 | 8.4634×10^{-3} |
| 40 | 250.35 | 2.8714 | 3.9957×10^{-3} |
| 45 | 264.164 | 1.491 | 1.9663×10^{-3} |
| 47.4 | 270.65 | 1.1022 | 1.4187×10^{-3} |
| 50 | 270.65 | 7.9779×10^{-1} | 1.0269×10^{-3} |
| 51 | 270.65 | 7.0458×10^{-1} | 9.0690×10^{-4} |
| 55 | 260.771 | 4.2525×10^{-1} | 5.6810×10^{-4} |
| 60 | 247.021 | 2.1958×10^{-1} | 3.0968×10^{-4} |
| 65 | 233.292 | 1.0929×10^{-1} | 1.6321×10^{-4} |
| 70 | 219.585 | 5.2209×10^{-2} | 8.2829×10^{-5} |
| 72 | 214.263 | 3.8362×10^{-2} | 6.2374×10^{-5} |
| 75 | 208.399 | 2.3881×10^{-2} | 3.9921×10^{-5} |
| 80 | 198.639 | 1.0524×10^{-2} | 1.8458×10^{-5} |
| 86 | 186.87 | 3.7338×10^{-3} | 6.958×10^{-6} |
| 90 | 186.87 | 1.8359×10^{-3} | 3.416×10^{-6} |
| 91 | 186.87 | 1.5381×10^{-3} | 2.860×10^{-6} |
| 100 | 195.08 | 3.2011×10^{-4} | 5.604×10^{-7} |
| 110 | 240 | 7.1042×10^{-5} | 9.708×10^{-8} |
| 120 | 360 | 2.5382×10^{-5} | 2.222×10^{-8} |
| 130 | 469.27 | 1.2505×10^{-5} | 8.152×10^{-9} |
| 140 | 559.63 | 7.2028×10^{-6} | 3.831×10^{-9} |
| 160 | 696.29 | 3.0395×10^{-6} | 1.233×10^{-9} |
| 180 | 790.07 | 1.5271×10^{-6} | 5.194×10^{-10} |
| 200 | 854.56 | 8.4736×10^{-7} | 2.541×10^{-10} |
| 250 | 941.33 | 2.4767×10^{-7} | 6.073×10^{-11} |
| 300 | 976.01 | 8.7704×10^{-8} | 1.916×10^{-11} |
| 350 | 990.06 | 3.4498×10^{-8} | 7.014×10^{-12} |
| 400 | 995.83 | 1.4518×10^{-8} | 2.803×10^{-12} |
| 450 | 998.22 | 6.4468×10^{-9} | 1.184×10^{-12} |
| 500 | 999.24 | 3.0236×10^{-9} | 5.215×10^{-13} |
| 550 | 999.67 | 1.5137×10^{-9} | 2.384×10^{-13} |
| 600 | 999.85 | 8.2130×10^{-10} | 1.137×10^{-13} |
| 650 | 999.93 | 4.8865×10^{-10} | 5.712×10^{-14} |
| 700 | 999.97 | 3.1908×10^{-10} | 3.070×10^{-14} |
| 750 | 999.99 | 2.2599×10^{-10} | 1.788×10^{-14} |
| 800 | 999.99 | 1.7036×10^{-10} | 1.136×10^{-14} |
| 850 | 1000 | 1.3415×10^{-10} | 7.824×10^{-15} |
| 900 | 1000 | 1.0873×10^{-10} | 5.759×10^{-15} |
| 1000 | 1000 | 7.5138×10^{-11} | 3.561×10^{-15} |