第1章 地震
2. 地震の大きさ
| 目次 | |
| a. | 震度 |
| b. | マグニチュード |
| c. | マグニチュードと地震の数 |
| d. | マグニチュードとエネルギー |
| 用語と補足説明 | |
a.震度
地震のたびにそのゆれ方が違うことは、日常的に経験している。地震のときのある場所でのゆれの程度表わす尺度が震度である。日本では震度0〜震度7まで、ただし震度5と、震度6は“強”と“弱”にわけられているので、全部で10段階ということになる。この中で、震度0はゆれなかったのではなく、地震計にだけ感じて、人体には感じない程度のゆれである。
以前気象庁は、職員の体感と周囲の状況で震度を決めていた。しかし震度計の開発により、1996年以降は震度は計測震度計という機械によって測られている。
震度とゆれの程度、ライフラインに与える影響などは、気象庁の「震度階級関連解説表」を参照。
震度はある場所でのゆれの程度なので、ある一つの地震に対しても、観測した(地震に遭遇した)場所が異なれば、震度も異なる(ことが多い)。一般に、震源に近い方が震度は大きくなるので、震度は震源(震央)を中心とした同心円上に分布する。しかし、震源からの距離が同じでも、地盤の性質などにより震度が大きく異なることがある。また、震源から遠いところにゆれの中心があるという異常震域という現象が起こることもある。
震度は必ず地名とともに表現される。例えば、「今回の地震では東京で震度3、横浜で震度2、千葉で震度2でした。」などという具合である。
b.マグニチュード(M)
震度ではある場所のゆれの程度を表わしているだけので、地震そのものの大きさはわからない。そこで、地震そのものの大きさを表わす尺度として考え出されたのがマグニチュードである。じつは、下に書いたようにマグニチュードの定義はいろいろあるし、誤差も大きいので、あまり小さな数字の違いには意味がないと考えた方がいい。
光で光源そのものの明るさがカンデラ、照らされているある面の明るさがルクスである。だから、マグニチュードがカンデラにあたり、震度がルクスに当たると考えてよい。
目安としては、マグニチュードが7を越えたら大地震、8を越えたら巨大地震である。1995年の兵庫県南部地震のマグニチュードは7.3、1923年の関東大地震のマグニチュードは7.9である。
(1) リヒターのローカルマグニチュード(ML)
リヒター・スケールともいう。アメリカ西部の地震を研究していたリヒター(アメリカ、1900年〜1985年)が、このスケールを1935年に提唱した。「震央から100kmの地点に置かれた標準地震計(ウッド・アンダーソン型地震計、倍率2800倍)の記録の最大振幅(μm)の常用対数」という定義である。もちろん、震央から100kmのところに運良く標準地震計が置かれている可能性はほとんどないので、他の場所の記録をもとにそこに標準地震計があったと考えて換算するわけである。
常用対数を取るということは、振幅が10倍になるとマグニチュードは1大きくなることである。ちなみに、最大振幅が1umでML=0、1mmでML=3、1mでML=6、1kmでML=9ということになる。つまり、実際には大きな地震になると、標準地震計では針が振り切れてしまう。だから、このリヒターのローカルマグニチュード(ML)は、あまり大きな地震ではなく、震源も比較的近い地震に対してよく使われる。
このリヒターの常用対数を使うというアイデアは、他のマグニチュードの定義にも影響を与えている。
(2) 実体波マグニチュード(Mb)と表面波マグニチュード(Ms)
リヒターのローカルマグニチュードでは、地震のエネルギーが正確に反映できないということで、最大振幅以外に、波の周期、震源までの距離や深さなども加味して求めるのが実体波マグニチュード(Mb)である。実体波とはP波、S波のことである。
一方、大地震では遠くまで伝わる長い周期(周期20秒)の表面波の最大振幅からマグニチュードが定義された。これが表面波マグニチュード(Ms)である。
上の定義から、実体波マグニチュードは比較的震源が深い地震に、表面波マグニチュード(Ms)は大地震に対してよく用いられていた。
(3) 気象庁マグニチュード(Mj)
気象庁は、独自のマグニチュードのスケールを使っている。これを気象庁マグニチュード(Mj)という。もちろん、上のマグニチュードの定義から求められた数値とは大きく違わないようにしている。
(4) モーメント・マグニチュード(Mw)
大地震に対して適用される表面波マグニチュードも、巨大地震の大きさが反映できていないという問題点が指摘されてきた。どんな大きな地震でも、Ms8.5くらいで頭打ちになってしまうのだ。そこで、金森博雄(当時カリフォルニア工科大学)は、地震を起こす力(モーメント)でマグニチュードを定義することを提唱した(1977年)。地震を起こす力(モーメント)をもとに決めるので、それ自身に物理的な意味があるし、大きな地震の大きさもきちんと反映できる。
例えば、表面波マグニチュード(Ms)では同じ8.5という三陸地震(1933年)と、チリ地震(1960年)では、地震の原因となった断層の規模がまるで違う。三陸地震を起こした断層は長さは約185km、断層のずれは約3.3m、これに対しチリ地震の断層の長さは約800km、断層のずれは約20mといわれている(下図参照)。モーメント・マグニチュード(Mw)では三陸地震は8.5、チリ地震は9.5となり、その大きさの違いが反映される。

日本付近で起こる大地震の断層と1960年チリ地震の断層
東京大学地震研究所吉井敏尅氏のページ
http://wwweprc.eri.u-tokyo.ac.jp/CSS/magnitude.html
今日ではモーメント・マグニチュード(Mw)は、世界中で大きな地震のマグニチュードの標準となっている。金森が提唱したので、カナモリ・スケールともいう。気象庁も大きな地震に対しては、気象庁マグニチュード(Mj)とモーメント・マグニチュード(Mw)を併記して発表するようになった。ただし、モーメント・マグニチュード(Mw)を求めるには少し時間がかかるので(震源の解析が必要)、速報段階では発表されない。
この100年間の巨大地震とそのモーメント・マグニチュード
| 地震が起きた年 | 地震名 | マグニチュード(Mw) |
| 1960年 | チリ地震 | 9.5 |
| 1964年 | アラスカ地震 | 9.2 |
| 1957年 | アリューシャン地震 | 9.1 |
| 2004年 | スマトラ島沖地震 | 9.0 |
| 1952年 | カムチャッカ地震 | 9.0 |
| 2011年 | 東北地方太平洋沖地震 | 9.0 |
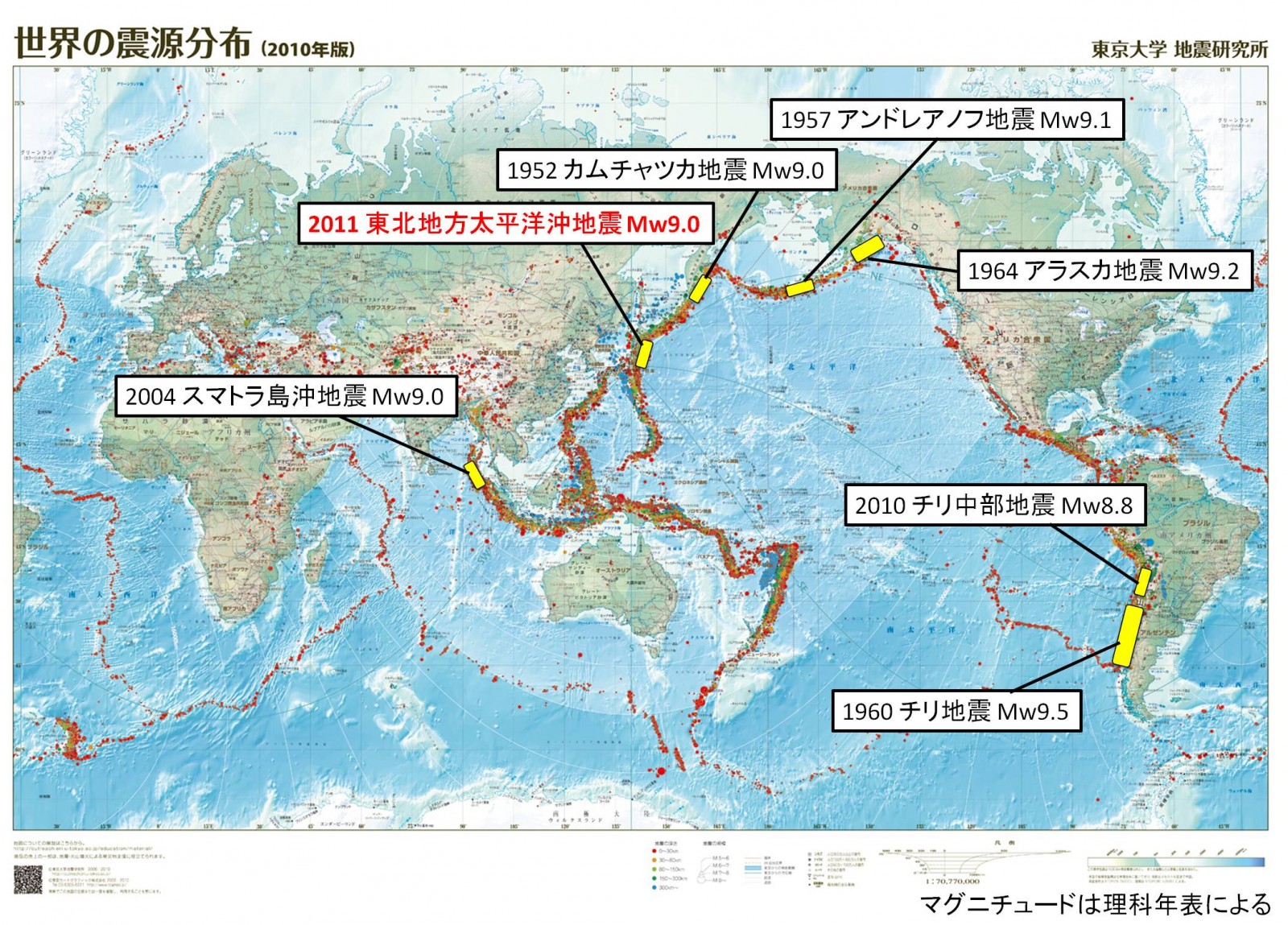
東大地震研:http://outreach.eri.u-tokyo.ac.jp/eqvolc/201103_tohoku/#largesteq
なお、マグニチュードについては、日本地震学会Web版広報誌「なゐふる」55号(2006年5月)も参照。2011年3月11日の東北地方太平洋沖地震のMwについては、9.1というハーバード大学の解析もある。http://www.globalcmt.org/CMTsearch.html(検索サイト)
当たり前だが、地震の統計を取ると、マグニチュードが大きな地震ほど数が少ない。おおよその目安として、マグニチュードが1大きくなると、地震の数は約1/10になる。つまり、マグニチュード5の地震が1000回起こる間に、マグニチュード6の地震は100回、マグニチュード7の地震は10回、マグニチュード8の地震は1回起こることになる。
このままでいくと、マグニチュード5の地震が10000回起こる間にマグニチュード9の地震が1回、マグニチュード5の地震が100000回起こる間にマグニチュード10の地震が1回ということになる。しかし、どうも地震のマグニチュードには上限があるらしく、チリ地震のMw9.5あたりが最大といわれている。だから、日本全体が一挙に壊滅するような超巨大地震を心配する必要はない。
マグニチュードが大きな地震ほど、大きなエネルギーを放出する。しかし、地震の際に放出されるエネルギー自体、それを求めることは非常に困難である。地形を変動させたエネルギーもあるだろうし、波となったエネルギーもある、熱となったものもあるかもしれない。つまり、地震のエネルギー自身を求めることは大変に難しい。さらに、マグニチュードの値もそれほど厳密な数値ではない。だから、マグニチュードとエネルギーの関係も、おおよその関係であると捉えておかないといけない。
おおよその関係でいうと、マグニチュードが1つ大きくなると地震のエネルギーは約30倍、マグニチュードが2つ違うと地震のエネルギーは約1000倍(≒30×30倍)、マグニチュードが3つ大きくなると地震のエネルギーは約30000倍(≒30×30×30倍)になる。
つまりマグニチュード8の地震のエネルギーは、マグニチュード5の地震のエネルギーの約3万倍のエネルギーを持っている。だから、もしどこかにすでにマグニチュード8の地震を起こすだけのエネルギーがたまっているとして、マグニチュード5程度の地震を人工的に起こし、それで地下にたまっているエネルギーを解放しようとすると、マグニチュード5の人工地震を3万回も起こさなくてはならない。毎日1回人工地震を起こすとして3万日(約82年)もかかることになる。人工的に、地下のエネルギーを解放するのは現実的でないことがわかる。
あまりいいたとえではないが、広島に落とされた原爆はマグニチュード6に相当するといわれているので、その程度のものを毎日1回爆発させて、それを8年くらい続けないとマグニチュード8の地震のエネルギーに相当しない。
いずれにせよ、マグニチュードが1大きくなると、地震の数は1/10に減っても、1つの地震のエネルギーは30倍になるので、これを合わせて考えると、マグニチュードが1大きな地震によって、3倍ほどのエネルギーが解放されていることになる。ようするに地下にたまっているエネルギーは、おもに大地震によって放出されていることになる。
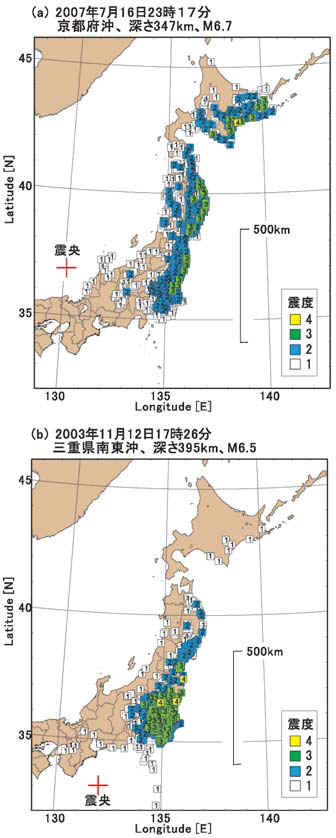
異常震域:震源から離れたところに、ゆれの中心(震度の中心)があるというもの。下図の左が異常震域で、上は若狭湾沖に震央があるのに、東北地方の太平洋側で強く揺れている。下も震央は紀伊半島沖なのに、東北地方の太平洋側で強く揺れている。
こうした異常震域を示す地震の共通した性質は、震源の深さが深いということである。上の地震の震源の深さは347km、下の地震の震源は395kmもある。400kmとすると、東京−大阪、あるいは東京−盛岡程度の距離になる。
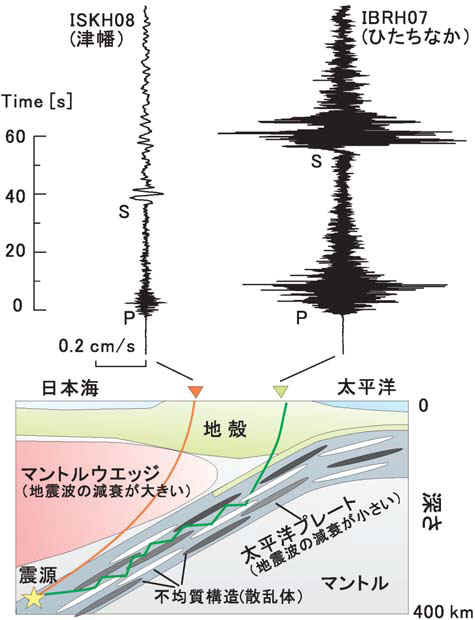
この現象は、下図のように日本列島は、冷たくて堅い太平洋のプレートが沈み込んでいる場所であるとすると理解できる。つまり、こうした震源が非常に深い地震の場合、冷たくてかたいプレート中を伝わる地震波は減衰が小さいので、距離が遠い東北の太平洋側(図ではひたちなか)まで伝わっても地震波はあまり弱くならない。一方、日本海側(図では津幡)は距離は近いのだが、途中で減衰の大きな部分(ちょっと温度が高くて柔らかい部分)を通らなくてはならないので、それだけ地震が弱くなってしまう。
こうした異常震域現象が、マントルの構造によるものだと最初に明らかにしたのは宇津徳治で、1966年のことである。今から考え直すと、これは日本列島の下に潜り込んでいるプレートを見つけたことになるが、そこまでいえなかったのは残念なことであった。
異常震域を起こす地震波についてもう少し詳しく見てみると、短周期成分(カタカタという揺れ、周期05秒以下)が卓越していて、しかもその揺れが長く続く、一方、長周期成分(ゆらゆらとした揺れ、周期0.5秒以上)はそれほどでもないか、かえって小さいくらいである。こうしたことは、単にプレートが1枚の固い岩盤ということでは説明できず、硬い岩石と柔らかい岩石が薄く交互に積み重なった状態になっていると考えると(下図)、その中で短周期の地震波だけが反射・屈折(散乱)を繰り返すことによってエネルギーが閉じ込められて地震波が弱められずに遠くまで伝わる、また散乱を繰り返すことによって地震波の波群が伸びて揺れが長く続くようになる、とうまく説明がつく。
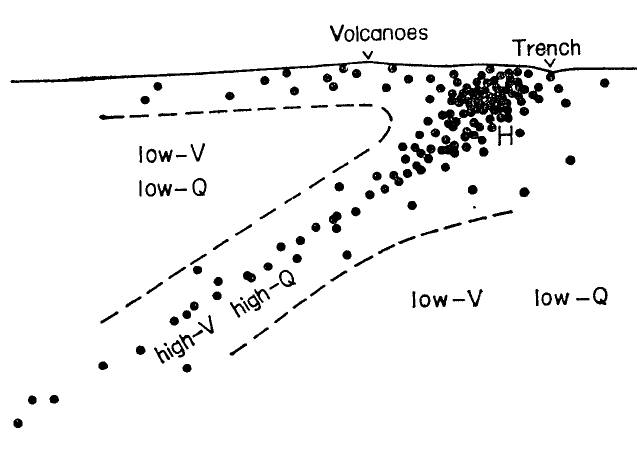
もう一つ、異常震域を起こす地震波は伝わる速さが速いという特徴もある。これは1960年〜70年代、気象庁が求めた震源位置と、世界中の地震データを使って震源を求めていた機関(CGS)が求めた震源位置について、気象庁が求めた震央位置の方が海溝側に寄り、深さも浅めに求まる、そのずれの大きさが震源が深いほど大きくなるとという系統的なずれがあるということからわかった。つまり、気象庁は地震波の伝わる速さが速い沈み込むプレート内を伝わってきた地震波をおもに解析しているため、そうしたことを考慮せずに平均的なマントル内を伝わる地震波速度して計算すると、震源位置がどうして海溝寄りに、また浅めに求まってしまうことになる。つまり、気象庁とCGSの震源位置のずれには意味があり、これは逆に沈み込むプレートを見ていたことになる。宇津徳治の「high-V high-Q」モデル参照(下左図)。上に描いたように、沈み込むプレートそのものが見えていたことになる。
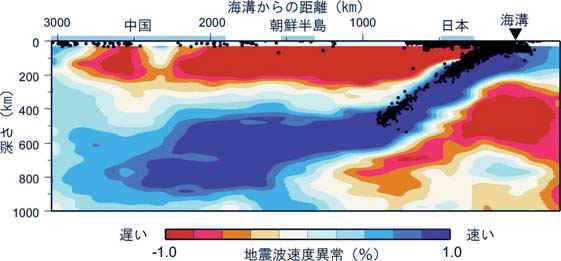
現在では、地震波CTによってこうした構造がはっきりとわかるようになった(下右図)。
 |
 |
| 異常震域の例と説明。日本地震学会「Web版なゐふる、第64号(2007年11月) http://www.zisin.jp/pdf/nf-vol64.pdf |
|
 |
 |
| 宇津徳治の「high-V high-Q」モデル。high-Vは地震波速度が速い、high-Qは減衰が小さいという意味。 https://www.jstage.jst.go.jp/article/zisin1948/22/1/22_1_41/_pdf |
潜り込んでいるプレート(スラブ)内を伝わる地震波は速い。 日本地震学会「Web版なゐふる、第63号(2007年9月)http://www.zisin.jp/pdf/nf-vol63.pdf |
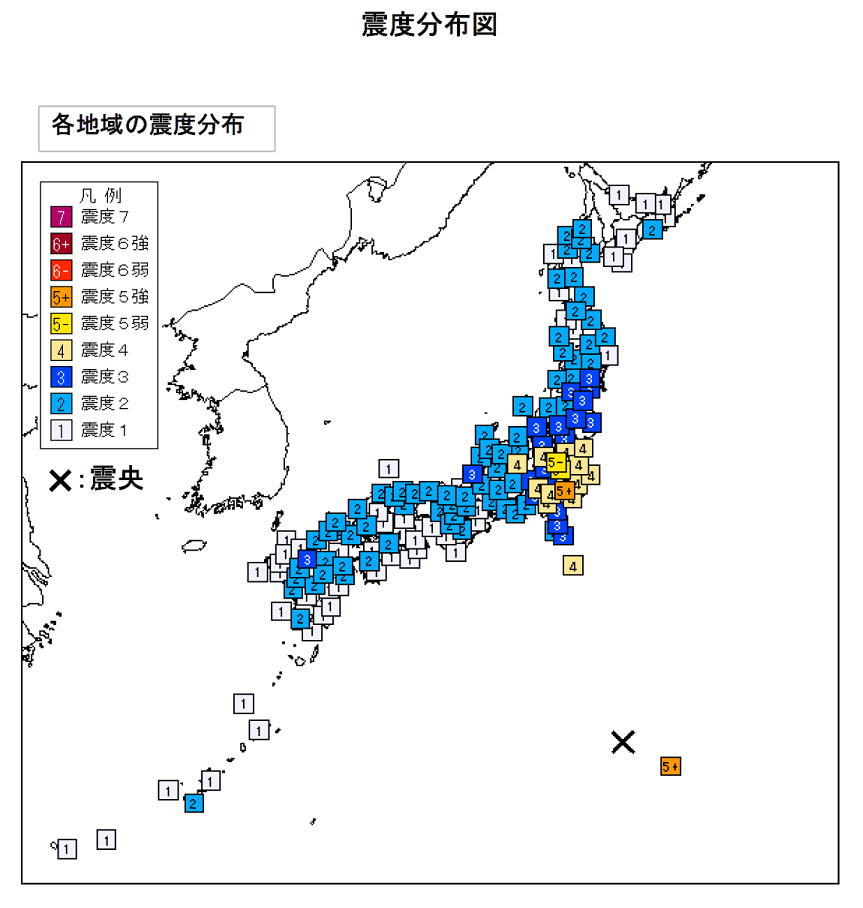
2015年5月30日の地震:小笠原諸島西方沖(北緯27°51.6′、東経140°40.9′)、深さ682km、Mj8.1(Mw7.9)という大地震が起き、日本中で震度1以上を観測した。このあたりで起こる深発地震の例に漏れず、異常震域を示した。この深さでM8クラスの地震は大変珍しいし、またたくさんの余震を伴ったことも珍しい。さらに今回の地震はこれまでの地震が起きている場所より100kmほど深いし、また東西に張力がはたらいて生じた正断層型の地震であったことも珍しい(このあたりの地震はプレートの沈み込み方向にはたらく圧縮力による逆断層型が多い)。ともかく、不思議な地震であった。ただ、マグニチュードは大きくても、震源がこれだけ深いので被害は出ていない(680kmは直線距離にすると東京-広島、東京−函館くらい)。
気象庁の解析では、地震を起こした断層は40km×40kmの大きさで、最大のずれは約6mとなっている。なお、気象庁は速報値としてまず震源の深さ590kmとし、後に682kmと訂正している。速報値は4カ所の観測点のデータのみを用いたとことなので、おそらく沈み込むプレート内を通過してきた地震波のみであったのだろう。プレート内は地震波速度が速いので、つまり走時が短かくなるので、見かけ上震源までの距離が近く、すなわち震源が浅く出てしまったと思われる。のちに、様々な場所でも観測値を用いることができるようになると、こうしたことはキャンセルされて、より本当の震源に近づいたのであろう。なお、USGS(アメリカ地質調査所)では、震央の位置北緯27.8386°、東経140.4931°、震源の深さ664km、Mw7.8としている。
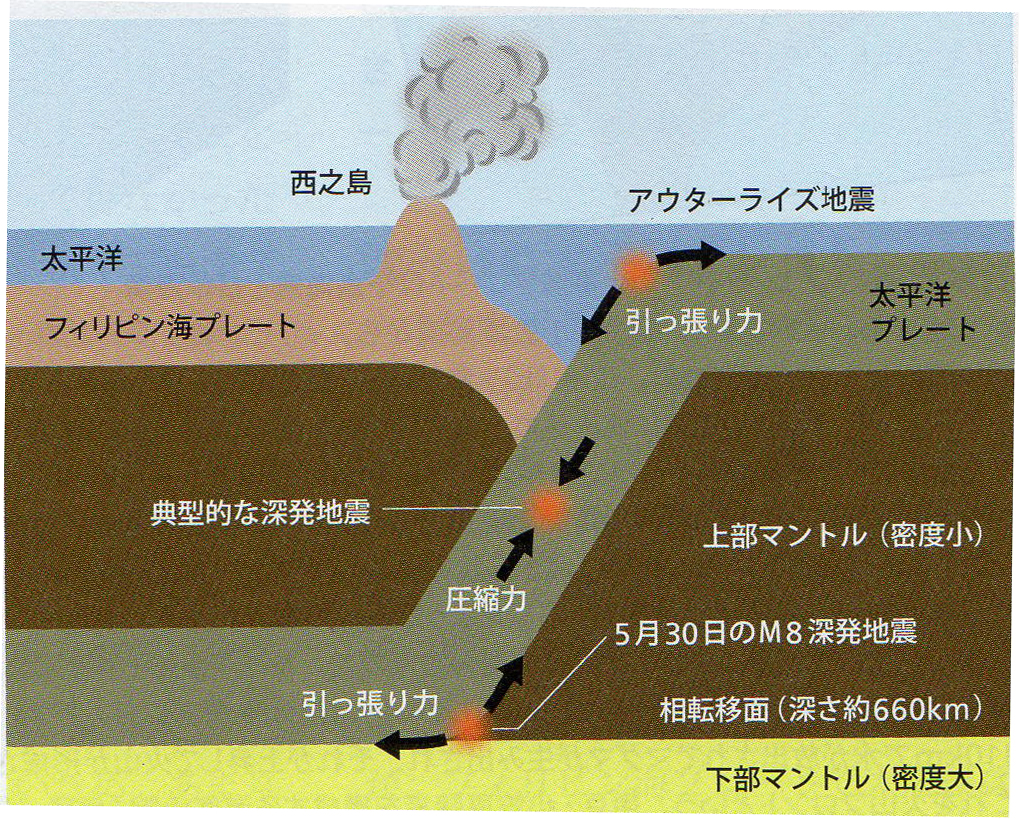
この地震が持つ意味についてはまだよくわかっていない。しかし、日経サイエンス2015年11月号にはJAMSTECの大竹政行氏の話を編集部(中島林彦氏)がまとめたものとして下の図のような解釈が紹介されている。すなわち、沈み込むプレートは660kmの深さ(マントルの岩石であるかんらん岩の主要構成鉱物であるかんらん石が相転移してスピネル構造になる深さ、ここでマントルの密度が急増する)に達すると、それ以上は潜り込めなくなって横たわるようになる、この横たわりが始まる部分は、ちょうどアウターライズ地震を起こす場所のように張力がはたらくため、今回のような正断層型の地震が起きたとするものである(下のサイエンスの図を参照)。震源が西之島の直下くらいであることも、何かを示唆しているのかもしれない。
 |
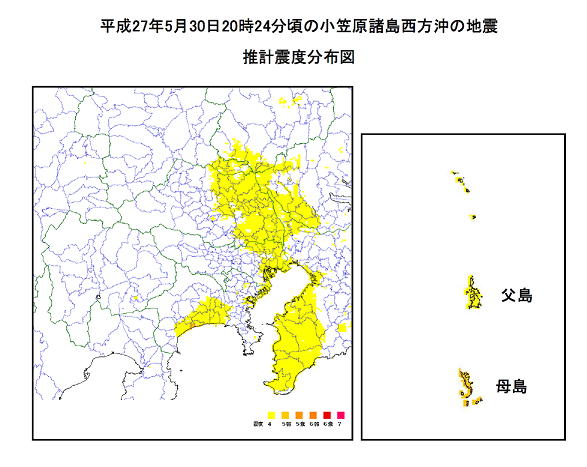 |
| 典型的な異常震域の震度分布。全国の震度分布と関東と小笠原の推計震度分布。神奈川のごく一部と母島で震度5強になっている。 http://www.jma.go.jp/jma/press/1506/08a/1505kanto-chubu.pdf |
|
.jpg) |
.jpg) .jpg) |
| USGS(アメリカ地質調査所)のデータベースから、父島付近の地震(1971年−2015年、北緯26°〜28°、東経138°〜145°、M>=3.0)のデータ(2186件)をダウンロードして、そのデータをExcelに読み込ませ、震源分布図(断面図)を作成。5月30日の震源位置が特異であることがわかる。 http://earthquake.usgs.gov/earthquakes/search/ |
http://csmap.jamstec.go.jp/を利用して、北緯27.8°・東経120度−北緯27.8°・東経155°の地震波CT図を作成。プレートの急角度での潜り込み、660kmくらいの深さでそれ以上沈めなくなって横たわる様子がよく見える。 使用モデル:GAP-P4 Obayashi, M., Yoshimitsu, J., Nolet, G., et al. (2013). Finite frequency whole mantle P wave tomography: Improvement of subducted slab images. Geophysical Research Letters 40: 5652-5657. (doi: 10.1002/2013GL057401) Fukao, Y., and Obayashi, M. (2013). Subducted slabs stagnant above, penetrating through, and trapped below the 660 km discontinuity. Journal of Geophysical Research, 118: 5920-5938. (doi: 10.1002/2013JB010466) |
 |
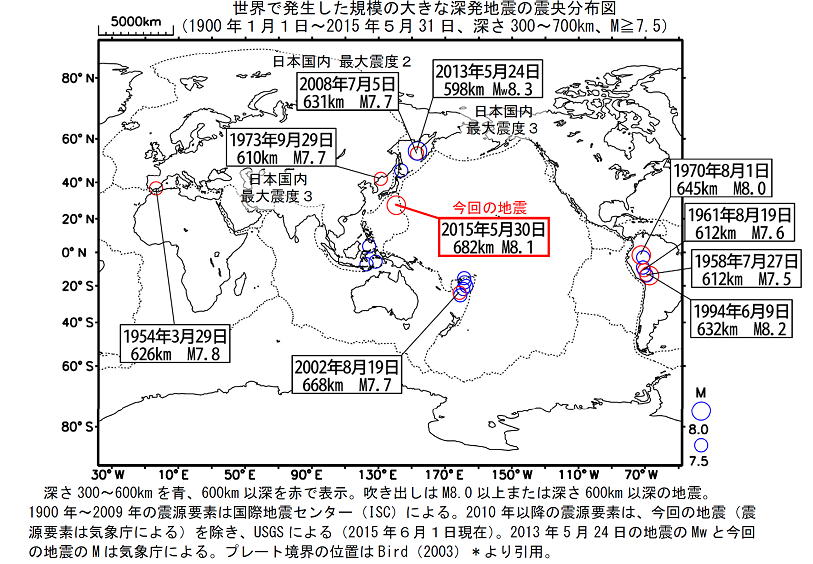 |
| 2015年5月30日の地震の解釈例(日経サイエンス2015年11月号) | 大きな深発地震の震源。プレートの沈み込み帯で起きている。 http://www.jma.go.jp/jma/press/1506/08a/1505kanto-chubu.pdf |
気象庁による詳しい報告は下のサイトを参照。
http://www.jma.go.jp/jma/press/1505/31d/201505311600.pdf
http://www.jma.go.jp/jma/press/1506/08a/1505kanto-chubu.pdf
チリ地震:チリ地震(1960年5月)は人類が観測した地震の中で最大のものといわれている。断層の大きさは800km×200km。この地震によって発生した津波は、途中のハワイを襲いながら約22時間半かけて太平洋を横断し、最大波高6mの波として日本(北海道、三陸、志摩半島、さらには沖縄)を襲った。この津波による犠牲者(死者・不明者)は日本全体で142名にもなった。
リヒター:リヒター(1900年〜1985)年はアメリカの地震学者。地震の規模の研究(マグニチュードの定義)や、地球の内部構造の研究を行った。

東京大学地震研究所「人工地震による地下構造調査」の「ちょっと一息」のページ
http://wwweprc.eri.u-tokyo.ac.jp/CSS/magnitude.html
マグニチュードと地震の数の関係式:対数(log)を使うと、あるマグニチュード(M)の大きさの地震の数(N)の間には、おおよそlogN=a−bMという関係が成り立つ。bの値は大きな地震と小さな地震の割合を示す。bが大きければ相対的に小さな地震の数が多く、bが小さければ相対的に大きな地震が多いということになる(もちろん絶対数は小さな地震の方が多い)。bの値は統計を取る期間や地域によって異なるが、だいたい0.9〜1くらいの値になる。bが1ならば、マグニチュードが1大きくなると地震の数は1/10となる。具体的なデータと、それから求めたグラフや式はこちらを参照。
マグニチュードとエネルギーの関係式:よく使われる式は、エネルギーE(J)、マグニチュード(M)とすると logE=4.8+1.5M という関係式である。対数の説明を見てもらえばわかるが、これは、マグニチュード(M)が1大きくなると、エネルギーは101.5倍になるということを示す。101.5=101×100.5=10×√(10)=31.5なので、マグニチュードが1大きくなると約30倍(32倍)という数値になる。
この式を使うと、マグニチュードが0.1大きくなるとエネルギーは1.4倍、0.2大きくなると2.0倍、0.3大きくなると2.8倍、0.4大きくなると4.0倍、0.5大きくなると5.6倍、0.6大きくなると7.9倍、0.7大きくなると11倍、0.8大きくなると16倍、0.9大きくなると22倍ということになる。しかし、本文に書いたように、こうした細かい数値にはあまり意味がない。あくまでも目安である。
具体的な数字と、火山噴火のエネルギーとの比較はこちらを参照。