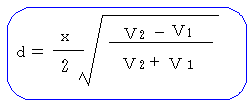
第3章 地球の構造-1- 付録:モホ不連続面の深さを求める
| (0) 仕様 |
| (1) 直接波(V1)と屈折波(V2)を見分ける |
| (2) V1、V2とLを求める |
| (3) グラフを確認する |
| (4) 求めた数値の評価 |
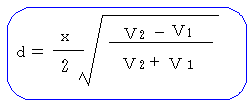
上の式を使って、実際のデータからモホ面を求めてみる。まず、Microsoft Excelファイルmohomen-hogo.xlsを開く。なお、このファイルの動作は、Macでは確認していません。
※ モホ不連続面までの深さをExcelを利用して求めるこの方法は、神奈川県立柏陽高校の山本明利氏(YPC(横浜物理サークル)の天神さん)の「モホロビチッチ不連続面を発見」をもとに、山賀が変更したものである。
(0) 仕様
a. シート
シートはグラフとデータの2枚を使う。
b.データ
黄色のセル内(A9〜B24)が走時のデータである。
c.操作するところ
ピンク色のセル内(C9〜C24とC28〜D29)だけを操作して、データとグラフを一致させる。
近似式はC28:D29内に埋め込まれている式を利用する。
d.結果
結果は、水色のセル(C3〜C5)に出る。
(1) 直接波(V1)と屈折波(V2)を見分ける。
はじめの方のデータと終わりの方のデータの2つぐらいから始め、近似直線がどのように変化するかを見ていく。
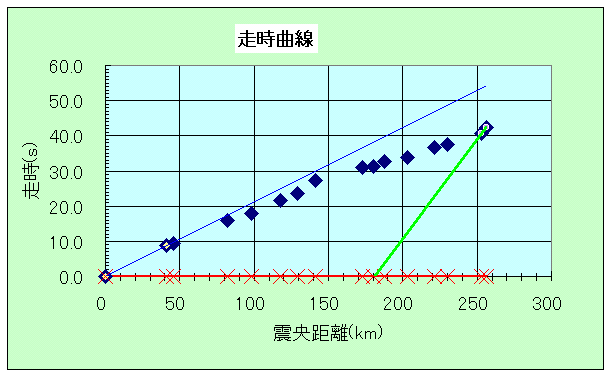
まずデータシートのデータ、B9-B10の値をC9-C10に、データB24-B23の値をD24-D23をコピーして見る。いろいろなセルに<#VALUE!>という表示が出るが気にせずに、グラフシートを見てみる。直接波は紺色で、屈折波は緑色で近似直線が引かれているが、全然データが反映されていないのがわかる。
そこで、データの範囲を上下にのばしていく。V1を求めるセルC11→C12→C13→…にB11→B12→B13→…をコピーし、またV2求めるをセルD22→D21→D20→…にB22→B21→B20→…をコピーするという具合である。そのとき、C9、D24に埋め込まれている式を、<コピー>→<形式選択して貼り付け>→<数式>でコピーしていくと簡単である。あるいは、データの数が少ないので、直接値を入力してもよい。
するとだんだん、近似直線がデータに合ってくることがわかる。
 |
 |
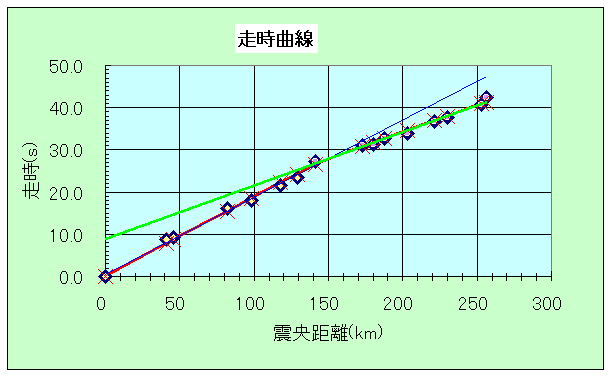 |
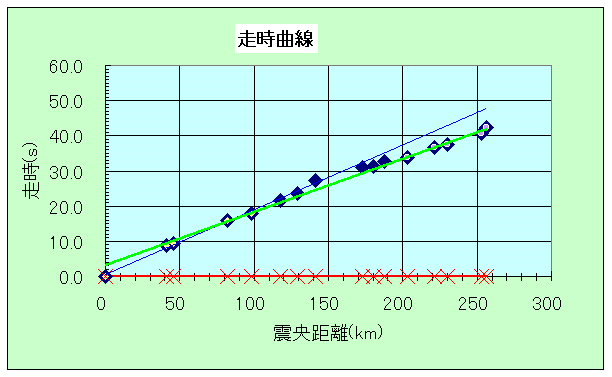
| V1としてC9〜C10、V2としてD24〜D23を指定してみる。 | V1としてC9〜C13、V2としてD24〜D18を指定してみる。 | V1としてC9〜C16、V2としてD24〜D16を指定してみる。 |
それぞれをどこまでのばすかはグラフを見ながら決める。たとえば、B9-B16をC9-C16に、B24-B17をD24-D17にコピーしてグラフを見ると、かなりよく近似されているように見える。
※ ただ、このへんは微妙で、(A16,B16)はV2を求める方(屈折波)に、あるいは両方に入れてもいい。見本ファイルでは(A16,B16)は、直接波・屈折波のもとになるデータの両方に入れてある。
※ ピンク色のセル(C9:D24)以外のセルは、変更できないようにしてある。
(2) V1、V2とLを求める
上で描いたグラフをプリントしたりして、物差し(定規)で長さを測りV1、V2を求めてもよい。しかし、せっかくExcelを使うのだから、近似式(V1とV2)そのものもExcelの関数linestを使って求めてみる。ただし、linest関数は「配列数式」なので、入力には注意が必要である。
見本ファイルでは、C9-C16を使ってV1(の逆数)とy切片(0)を求める式をC28-D28に、D16-D24を使ってV2(の逆数)とy切片を求める式をC29-D29に入れある。式を見ると両端に{ }がついている。これが配列数式のしるしである。配列数式は最後に[Shift][Ctrl][Enter]を同時に押すことによって入力される。両端の{ }は自動的に挿入される。
これによって求まったC28とC29の値は、それぞれV1とV2の逆数である。そこで、C31とC32でV1とV2を求めている。さらにC33では、C28、C29、D29の値から、走時曲線が折れ曲がる観測点までの距離(L)を求めている。最後にD34には、V1(C31)、V2(C32)と走時曲線が折れ曲がるまでの観測点の距離L(C33)から、モホロビチッチ不連続面までの深さを求める式によってその深さを求めている。
C3にはC34、C4にはC31、C5にはC32の値がコピーされている。このC3の値が、求めるモホ不連続面までの深さである。
※ もし、V1、V2の近似式を求める範囲を変えたければ以下のようにする。例えばV1を求めるデータをB9〜B15に、V2を求めるデータをB24〜B15にしてみる。C28に入力する式は =LINEST(C9:C15,A9:A15,FALSE) である。実際には埋め込んでいる式に対し、C16をC15に、A16をA15に変えればよい。そして最後に[Shift][Ctrl][Enter]を同時に押す。あとの、D28、C29、D29も同様に式を入力する。
(3) グラフを確認する
震源からの距離をグラフを見ると、V1のもととなるデータの系列(C9〜C16)、V2ももととなるデータ(C24〜D16)と、これらから求めたV1・V2の近似直線はデータによくあっている。さらに、シミュレーション(グラフの赤線)の値もデータに合っている。
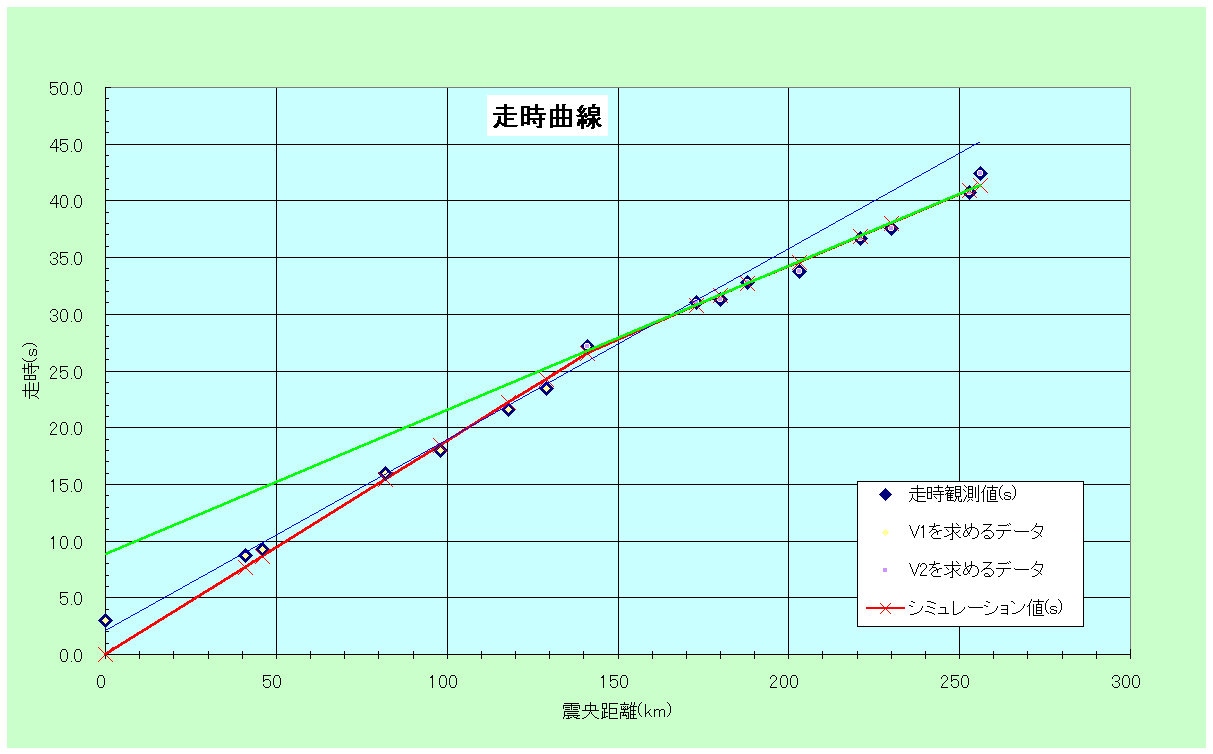
(4) 求めた数値の評価
これが、「絶対に正確な値、唯一の解」なのだろうか。試みにV1、V2のもととなる範囲をひとつずらして、(A15,B15)までをV1、それ以降をV2とすると、(2)の範囲ではd=31.7kmだったものが、d=32.2kmになってしまう。こちらもグラフ上では(2)で使った値と同じく非常によくデータに合っている。
これらから、実際の解析は非常に難しいし、当然かなりの誤差が含まれているということがわかる。