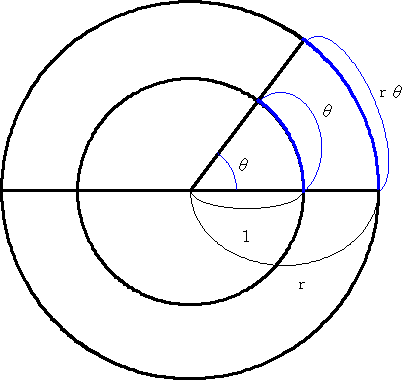
円の中心角とそれに対する弧の長さは比例する。この関係を使うと、弧の長さから逆に角度を決めることができる。半径1の円(単位円)を考え、ある弧の長さ(例えばθという長さ)に対する中心角をθと定義する。そして、この角度はrad(ラジアン)という単位で表す。このとき、半径r、中心角θradに対する弧の長さはrθとなる。

360°法との関係は、半径1の円の円周が2πで、その中心角が2π(rad)なので
360°= 2πrad
180°= π rad
90°=1/2πrad
60°=1/3πrad
45°=1/4πrad
30°=1/6πrad
また
1°=2π/360(rad)=1.74×10-2rad
1'(1/60)=2π/(360×60)=2.91×10-4rad
1"(1/60')=2π/(360×60×60)=4.85×10-6rad
半径1km(106mm)の円を考えると、1"=4.85×10-6radだから、その弧の長さは
106mm×4.85×10-6rad=4.85mm
いま、非常に小さい角度に対する三角関数(三角比)の値を考える。
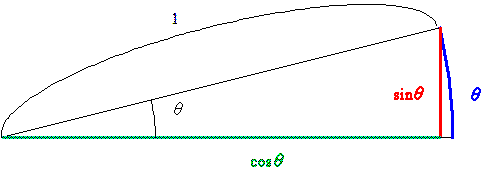
半径1の円に対し、角度θradに対するこの長さはθ(青い弧の長さ)、sinは赤線の長さ、cosθは緑線の長さであるので
θ→0 のとき sinθ→θ (赤い線の長さは青い弧の長さに近づく)
cosθ→1 (緑の線の長さは半径の1に近づく)
tanθ→θ (tanθ=sinθ/cosθ)
つまり、角度の単位でラジアン(rad)を使うと、角度が小さいときは三角関数の値は、三角関数表を引かなくともわかる。
たとえば、sin1"=sin(4,85×10-6)rad=4.85×10-6
cos1"=1
など。あとは、角度が小さいときは、角度の大きさとsinの値は比例することを利用すればよい。
sin10"=sin(4,85×10-6×10)rad =4,85×10-5
sin(0.5)"=sin(4,85×10-6/2)rad=2.43×10-6
など。
簡単にいうと、θradのθの値がすごく小さいときは、角度とsin(tan)の値は比例することになる。