第5章 重力(2)
| 目次 | ||
| 3. | 重力異常 | |
| a. | 重力異常 | |
| b. | 高度補正(フリーエア補正)とフリーエア異常 | |
| c. | 地形補正 | |
| b. | ブーゲ補正とブーゲ異常 | |
| 4. | 重力異常の意味 | |
| a. | フリーエア異常 | |
| b. | ブーゲ異常 | |
| 用語と補足説明 | ||
| この章の参考になるサイト | ||
3. 重力異常
実際に測定した重力(g)とその場所(緯度)での正規重力(g0)の差を、重力異常(Δg0)という。
Δg0=g−g0
だが、正規重力は地球だ円体上での理論的な重力である。実際に測定した場所は、地球だ円体上にはないことが多い。また、斜面で測定することもある。だから、実測重力gを単純に標準重力g0と比較しても意味はない。何らかの方法で、実測重力gを地球だ円体上(おおよそ海抜0m)の値に換算して比較しなくてはならない。これは、測定した各地の気圧を比較するときに、海抜0mでの値に換算する海面校正と同じ考えである。
なお、重力の測定の仕方については、下の国土地理院の<重力>のページの中の<国土地理院の重力測量>参照。
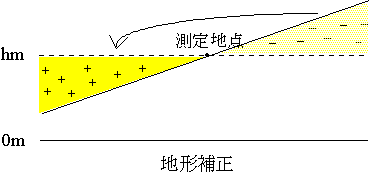
標高hmの地点は海抜0mの地点よりhmだけ地球の中心からの距離が遠い。つまりその分だけ引力が小さくなっているはずである。この距離の差の分を補正するのが、高度補正である。
高度補正では、海抜0mからhmまでの間には何もない(空気(フリーエア)だけ)と考えて補正する。

高度補正(フリーエア補正)によって実測重力gはg1という値に補正される。この高度補正された実測重力(g1)と正規重力(g0)の差(Δgf)を、フリーエア異常(フリーエア重力異常)という。
フリーエア異常: Δgf = g1−g0
c.地形補正
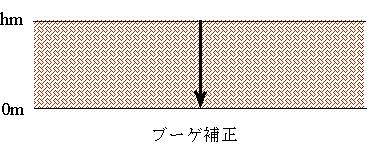
ふつう重力の測定を行う地点は、海抜0mでもないし、また平坦な地形でもない。そこでまず、地形を(仮想的に)平坦にならす。つまり、標高hmの高さで測定したとすると、そこを標高hmの広大な台地であるとして実測重力を補正する。
つまり、下図のような斜面で測定したとすると、そこより標高の高い部分の岩石による引力を受け、逆にそこより標高の低い部分は岩石と比べて質量が無視できる空気しかない。そこで、標高の高い部分の岩石を取り去り、標高の低い部分を岩石で埋めると考えるのである。地形補正の大きさは下を参照。
こうして、実測重力gは地形補正をするとg2となる。
d.ブーゲ補正とブーゲ異常(ブーゲー補正とブーゲー異常)
もう一つの高度による重力の変化を考慮して補正するのが、ブーゲ補正である。ブーゲ補正は、海抜0mからhmまでは、平均的な岩石(花こう岩、密度2.670×kg/m3)が存在しているとして、その岩石による引力を考慮して、実測重力を海抜0mの値に換算する。
高度補正(フリーエア補正)と地形補正された実測重力は、g2からブーゲ補正によってさらにg3という値に補正される。このブーゲ補正された実測重力(g3)と標準重力の差(Δgb)を、ブーゲ異常(ブーゲ重力異常)という。
ブーゲ異常: Δgb = g3−g0
※ ブーゲ(ピエール・ブーゲ、1698年〜1758年)については、ペルー(現エクアドル)の測量隊も参照。
4.重力異常の意味
a.フリーエア異常
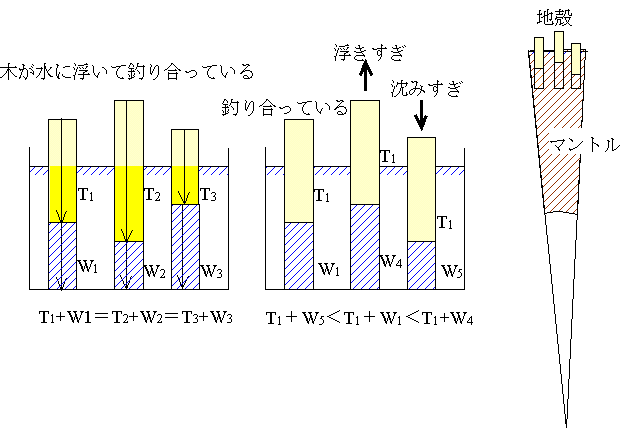
木が水に浮いている状態を考える。同じ種類の木の柱(密度が同じ木の柱)ならば、その高さにかかわらず、ある一定の深さでは木の柱+水の柱の重さは、どの木の下でも一定である。つまり、下の左図の左の木の柱の重さT1とその下の水の柱の重さW1を足したものは、真ん中の木の柱の重さT2とその下の水の重さW2を足したもの、右の木の柱の重さT3とその下の水の重さW3を足したもの、すべてが等しい。
これは、浮力はそのもの(木)が押しのけている水(下左図では濃い黄色の部分)の重さに等しいということを考えれば明らかである。
ところが、釣り合いの状態からずれている状態を考えると(下中図)、ある一定の深さでの木の柱の重さ+その下の水の柱の重さは、同じ高さの木の柱でも浮きすぎているときは水の柱が長くなる分だけ重くなり、沈みすぎていると水の柱が短くなる分軽くなることがわかる。
地殻は一般的にはマントルに浮いて釣り合っている。これをアイソスタシーという。木を地殻、水をマントルと考えれば、地殻がマントルに浮いて釣り合っていれば(アイソスタシーが成り立っていれば)、地球の表面から地球の中心までの地殻+マントル(さらには核)の柱の重さはどこでも等しいはずである。
だから、地球の表面に置いた物体にはたらく地球の質量は地殻が浮いて釣り合っていればどこでも同じ、つまり、地球の中心からの距離を同じすれば(例えば海抜0mにすれば)、その物体はたらく地球の引力はどこでも同じになるはずである。
ところが地殻が浮きすぎていると、地球の中心までの質量は、地殻が浮いて釣り合っている場所より大きくなる。そこで、地球の中心からの距離を同じにしてやると、その物体にはたらく地球の引力は大きくなる。ぎゃくに、地殻が沈みすぎていると、地球の中心までの質量は、地殻が浮いて釣り合っている場所より小さくなる。そこで、地球の中心からの距離を同じにしてやると、その物体にはたらく地球の引力は小さくなる。
このように考えると、質量の補正をしない、地球の中心からの距離(高度)だけを補正して得られる重力g1は地下の質量を反映していて、フリーエア異常(Δgf)は、その場所でアイソスタシーが成立しているかどうかを示すものであることがわかる。
Δgf=0 … アイソスタシーが成り立っている。
Δgf>0 … アイソスタシーが成り立っておらず、地殻が浮きすぎている。
Δgf<0 … アイソスタシーが成り立っておらず、地殻が沈みすぎている。
中央海嶺では、Δgf>0であることが多く、地殻が何か下から突き上げられていることを示す。また、海溝ではΔgf<0であることが多く、地殻が何か下に引きずり込まれていることを示す。日本のフリーエア異常は下を参照。
b.ブーゲ異常
ブーゲ異常は、標準的な岩石の密度を考えて高さも補正する。だから、そこで得られるブーゲ異常(Δgb)は地下の質量の大小ということになる。
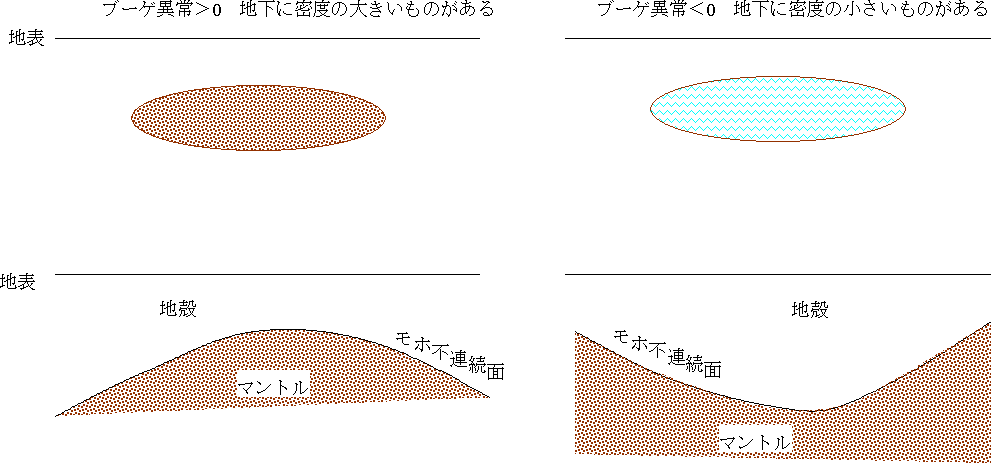
Δgb>0 … 地下の質量が平均より大きい。密度の高いものがある。
Δgb<0 … 地下の質量が平均より小さい。密度の小さいものがある。
ブーゲ異常が正(プラス)、つまり地下に密度の高いものがあるということは、例えば金属鉱床などがあるということも考えられる。もっと広範囲にブーゲ異常が正ならば、密度の高いマントルがマントルが盛り上がっている(モホ不連続面が浅い)ということを示す。
逆にブーゲ異常が負(マイナス)なら、地下に密度の小さい石油鉱床などがあるということも考えられる。もっと広範囲にブーゲ異常が負ならば、モホ不連続面が深いということになる。実際に大山脈ではブーゲ異常が負であることが多い。
また、断層などで急に地下の岩石の密度が変わっているときにも、それがブーゲ異常として現れることもある。
地殻、マントル、モホ不連続面などは地球の構造-1-、-2-を参照。
日本のブーゲ異常は下を参照。
※ ブーゲ(ピエール・ブーゲ、1698年〜1758年)については、ペルー(現エクアドル)の測量隊も参照。
高度補正(フリーエア補正)の値:地球の中心からの距離(つまり標高)が1m大きくなるごとに、重力は0.3086mgal(ミリガル)だけ小さくなる。逆に高さhmでの重力の値を海抜0mの値に換算するには、実測重力に0.3086mgal/mを加えればよい。
ここでgal(Gal、ガル)は小さな重力を表わす単位で重力異常などではよく使われる。1gal=1cm・s-2(10-2m・s-2)である。重力加速度は9.80665m・s-2であるから、重力加速度をgalで表わすと約980galということになる。なお、galの名はガリレオ・ガリレイ(イタリア、1564年〜1642年)に由来する。
地形補正の大きさ:広大な平地(大地)や海では地形補正の必要はない(補正量0)。日本のような山地が多いところでも数mmgal程度、凹凸の大きな場所(起伏の激しい場所)では数十mmgalになることもある。
高さと重力:高さhmでの重力は、海抜0nmのところと比べてどのくらい小さくなるだろう。同じ緯度では自転軸からの距離の大小による遠心力の大きさにはほとんど違いはない(そもそも遠心力は引力と比べて大変に小さい)ので、地球の中心からの距離の違い(hm)だけを考える。
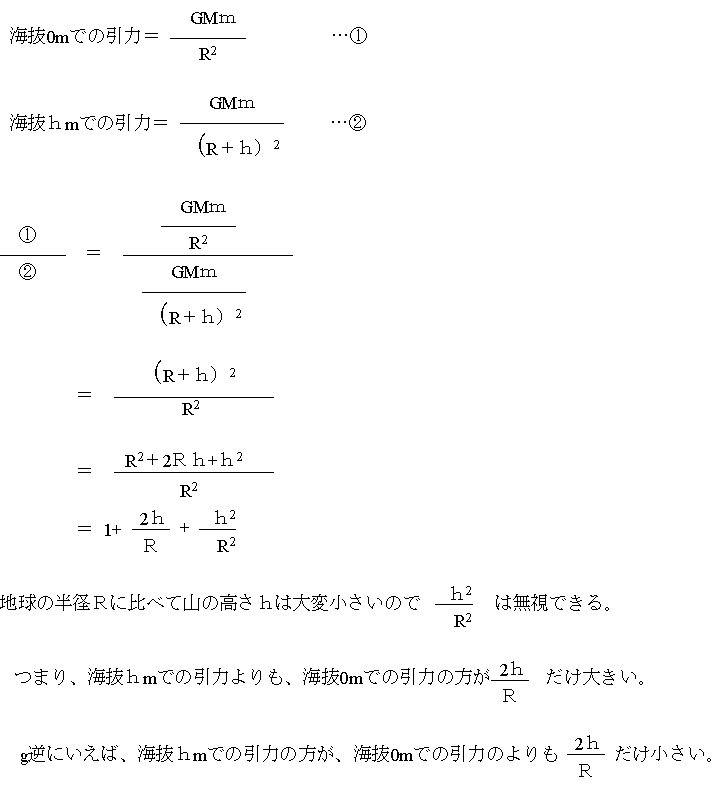
地球の半径6.4×106mに対し、1mの高さでは、(2×1÷6.4×106)だけ重力(引力)が小さくなる。重力加速度は9.8m・s-2(980gal)だから、高さ1mにつき重力加速度は3.06×10-6m・s-2(0.000306gal=0.306mgal)ずつ小さくなる。もう少し正確な数値を使うと上に書いたように、0.3086mgal(ミリガル)=3.086×10-6m・s-2ずつ小さくなる。
地球の半径を6400kmとすると、エベレスト(標高8884m=8.9km)の頂上では(2×8.9÷6400)=0.0028(約0.28%)、富士山(3776m=3.8km)の頂上では0.0012(0.12%)だけ重力が小さくなる。地球半径に対して切りのいい高さ3200m(3.2km)では0..1%(体重60.00kgの人が59.94kg=60gのダイエット!)、高さ1600m(1.6km)では0.05%(体重60.00kgの人が59.97kg=30gのダイエット!)に成功する?
さらに両極と赤道の重力の比でも計算したように、同じ海抜0mでも、赤道での重力は両極よりも約1%(1.03%)小さい。だから、赤道近くのの高い山ではもっと重力が小さくなる。例えば赤道直下で高さ1600m(1.6km)の高さの土地では、極地方より1.03%+0.05%=1.08%重力が小さい。極地方で体重60.00kgの人は、59.35kg(650gのダイエット!)になる。
これは微妙な数値ではあるが、限界を競うような場合、例えばオリンピック競技などでは意味のある数値かもしれない。実際、1968年には、標高2300mのメキシコシティ(メキシコ)で行われたことがある。メキシコシティは緯度も北緯20°程度であり、国際大会が開かれる場所としてはきわめて緯度が低い(それだけ重力小さい)。
メキシコシティは標高が高く空気が薄いので持久力を競う競技長距離走などは不利だった。しかし空気が薄いということは、空気抵抗が小さいというメリットがあるということであり、その分瞬発力を競う競技は有利だったといわれている。例えば走り幅跳びでは、当時としては驚異的な記録8.90mという世界記録が出ている(ビーモン選手)。これは1991年にパウエル選手が東京で8.95mを飛ぶまでの間、20年以上も破られなかった記録である。
こうした好記録が生まれたもう一つの要因として、重力の問題が少しかかわっているのかもしれない。
ブーゲ補正の値:海抜hmと海抜0mまでに存在している岩石の密度ρ、万有引力定数Gとすると、高さhmにつき2πGρhを補正を引く。
日本の重力異常:国土地理院の図(http://www.gsi.go.jp/atlas/archive/j-atlas-d_j_10.pdf)。サムネイル画像をクリックすると拡大します。戻るときはブラウザの戻るボタン。
 |
 |
| フリーエア異常。日本海溝で大きくマイナスになっている。日本列島中央部でのプラスは地形の影響が大きい。 | ブーゲ異常。日本列島中央部でマイナスになっていて、モホ面が深いことがわかる。東北〜西南日本の太平洋側は物質が押しつけられ付加体を形成しているためにプラスになっている。 |
測地学会:http://www.geod.jpn.org/web-text/part2/2-2/index.html
国土地理院(重力の測定のページ):http://www.gsi.go.jp/buturisokuchi/gravity_menu02.html